Bestimmen Sie die folgenden Integrale, wie erfahre ich u bei gegebenem x?

Question

Aufgabe: Bestimmen Sie die folgenden Integrale

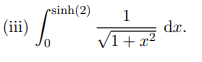
Hinweis für (iii): Substitution  x := sinh t

Text erkannt:

(iii) \( \int \limits_{0}^{\sinh (2)} \frac{1}{\sqrt{1+x^{2}}} \mathrm{~d} x \).

Problem/Ansatz:

In der Lösung steht x= sinh u, dx=cosh u du und u=arsinh x. Meine Frage:

Wie komme ich auf das u=arsinh x? Hängt das irgendwie damit zusammen das ich cosh u / cosh u habe? Ich brauche das ja um die Grenzen einzusetzen oder damit ich Rücksubstituieren kann.

Answer 1

Die Substitution gibt den Zusammenhang zwischen \(x\) und \(u\), hier \(x=\sinh u\). Wenn man \(u\) braucht, stellt man eben um, das geschieht durch Anwenden der Umkehrfunktion auf beiden Seiten; die von \(\sinh\) nennt sich \(\rm arsinh\), ergibt also \(u=\rm arsinh \it x\).

Genau das gleiche hast Du übrigens vor ein paar Tagen schonmal gefragt. Wenn Du es nicht verstehst, ist es völlig ok nochmal nachzufragen.

Comments

Ok das ergibt Sinn. Danke