Hallo,
Welche Funktion der Funktionsschar hat bei x = 3 einen Tiefpunkt?
Du sollst offenbar k so bestimmen, dass bei x = 3 ein Tiefpunkt ist
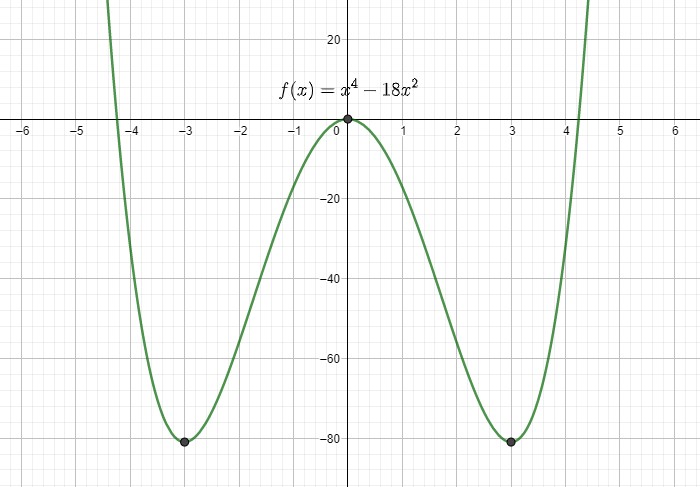
\(f_k(x)=x^4-kx^2\\ f_k'(x)=4x^3-2kx\\ f_k''(x)=12x^2-2k\)
Setze f'(x) = 0.
Du erhältst drei Lösungen, zwei davon in Abhängigkeit von k.
Setze 3 für x ein und löse nach k auf.
Gruß, Silvia