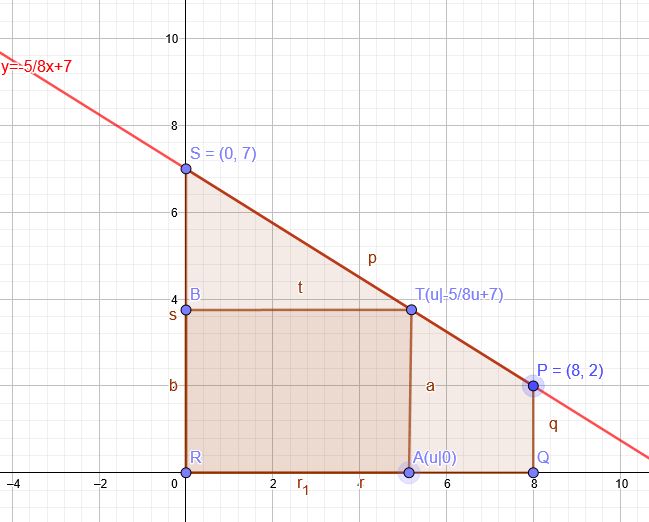
Geradengleichung SP:
\( \frac{y-2}{x-8}=\frac{7-2}{0-8}=-\frac{5}{8} \)
\( y=\frac{7-2}{0-8}=-\frac{5}{8} \cdot x+7 \)
\(A(u)=u \cdot (-\frac{5}{8} \cdot u+7) \)soll maximal werden.
\(A(u)=-\frac{5}{8}u^2 +7u \)
\(A´(u)=-\frac{5}{4}u +7 \)
\(-\frac{5}{4}u +7=0 \)
\(u= \frac{28}{5} \)
\(AT= - \frac{5}{8} \cdot \frac{28}{5} +7= - \frac{5}{8} \cdot \frac{28}{5} +7=3,5\)
\(A=3,5\cdot 5,6=19,6FE\)
