Es ist bei einer Abbildung y0 zu verschieben.
Hier zb ist f(40), bei der die ich heute probiert habe war f(20) 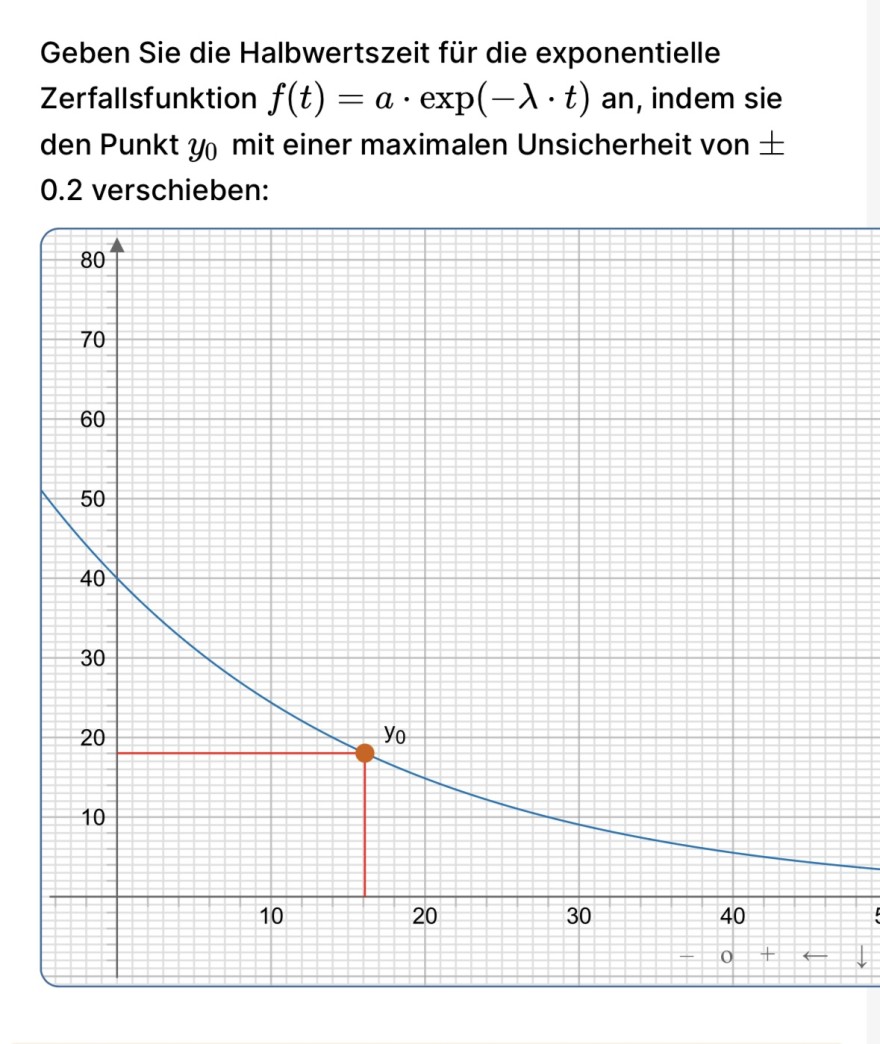
Text erkannt:
Geben Sie die Halbwertszeit für die exponentielle Zerfallsfunktion \( f(t)=a \cdot \exp (-\lambda \cdot t) \) an, indem sie den Punkt \( y_{0} \) mit einer maximalen Unsicherheit von \pm 0.2 verschieben: