Ist der Rechenweg und das Ergebnis richtig?
Wir behandeln momentan e-Funktionen und eine Teilaufgabe war es eine Stammfunktion zu f(x) anzugeben, und ich bin mir da noch sehr unsicher, ist dies richtig?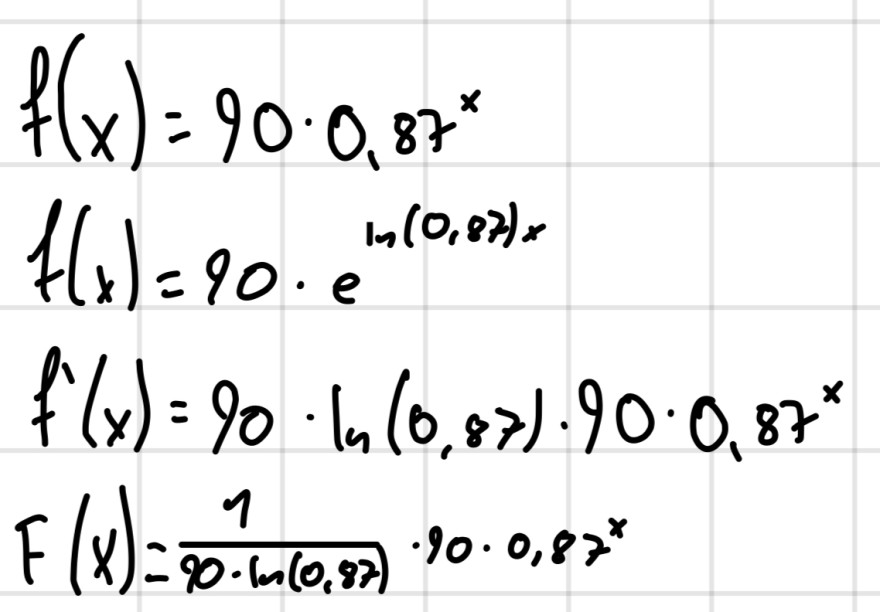
Text erkannt:
\( \begin{array}{l}f(x)=90 \cdot 0,87^{x} \\ f(x)=90 \cdot e^{\ln (0,87) x} \\ f^{\prime}(x)=90 \cdot \ln (0,87) \cdot 90 \cdot 0,87^{x} \\ F(x)=\frac{1}{90 \cdot \ln (0,877) \cdot 90 \cdot 0,87^{x}}\end{array} \)