 Aufgabe:
Aufgabe:
Sei \( K \subset \mathbb{R} \) nichtleer, kompakt und \( f: K \rightarrow K \) eine Funktion mit \( \mid f(x) - f(y) \mid < \mid x-y \mid \) für alle \(x,y \in K \). Zeigen Sie, dass f genau einen Fixpunkt \(x_{0} \in K \) besitzt.
Tipp: Satz über stetige Funktionen auf Kompakta.
Problem/Ansatz:
Hi Leute,
ich sitze gerade an der obigen Aufgabe und komme nicht darauf wieso das stimmen soll. Mit dem Satz auf Kompakta kann man begründen, dass f(x) gleichmäßig stetig ist und f(x) sein Maximum und Minimum in K annimmt.
Ich erhalte somit die Eigenschaften: kompakt, gleichmäßig stetig, Max/ Min in K und ggf. Abgeschlossenheit + Beschränkheit (S.v.Borell).
Die Eigenschaft \( \mid f(x) - f(y) \mid < \mid x-y \mid \) für alle \(x,y \in K \) sagt mir doch im Grunde, dass der Betrag meiner Steigung immer kleiner die der Identitätsabbildung f(x) = x bzw. f(x) = -x ist. Also -1<a<1, wenn a die Steigung ist.
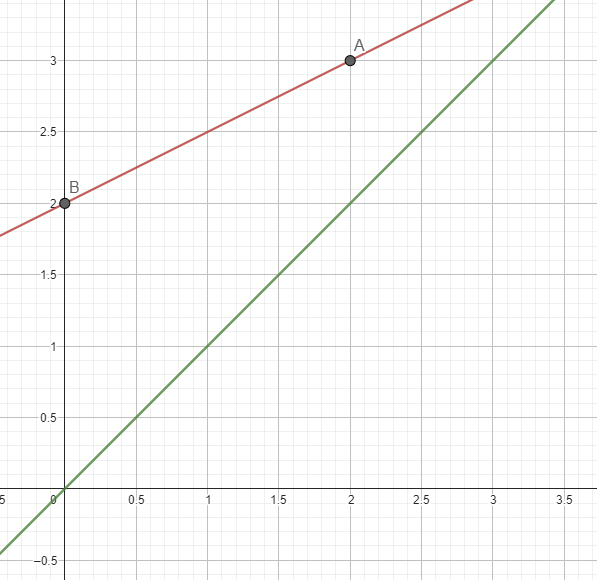
Nun wäre doch mit f(x)=0,5 x + 2 und \( K := [0, 2] \) K kompakt, f(x) stetig mit max f(x) = 3 und min f(x) = 2, aber es gäbe offensichtlich keinen Fixpunkt, da man sich immer über der Identität befindet.
Ich weiß, dass ich einen Denkfehler habe, aber ich verstehe nicht ganz wieso ^^
Über ein paar Tipps würde ich mich freuen.
LG Syntax