Wieso wird hier nicht mit 1 im Sinn gerechnet?

Question

Aufgabe:

Binäre Zahlen addieren

a)

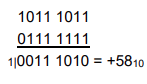hier wird mit 1 im Sinn gerechnet

b)

Text erkannt:

\( \begin{array}{r}10111011 \\ \underline{01111111} \\ 1 \mid 00111010=+58_{10}\end{array} \)

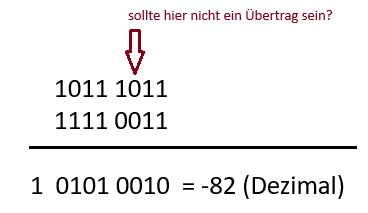
Wieso wird hier nicht mit 1 im Sinn gerechnet? Das ist die richtige Lösung.
Kann mir jemand erklären, wieso????

Comments

Ist jetzt das Bild relevant oder der Text?

---

Apropos (b):
Manchmal muss man auch zwei 1er im Sinn haben.

Wenn du die Überträge hinschreiben würdest, würde sich deine Frage von selbst beantworten.

Answer 1

Wenn das wirklich eine Addition im binären System ist, dann lautet das Ergebnis 110101110.

Comments

Wie soll 58 rauskommen, wenn 10111011 = 187 ist?

Um wie soll eine negative Zahl (-82) rauskommen?

Im Sinn meint wohl "1 gemerkt". So sagte man früher.

---

Wie soll 58 rauskommen, wenn 10111011 = 187 ist? Um wie soll eine negative Zahl (-82) rauskommen?

https://de.m.wikipedia.org/wiki/Zweierkomplement

---

Welche Relevanz hat das hier? Bitte so einfach wie möglich erklären.

---

Ich hab's. Es handelt sich um das BCD-System (hab ich vergessen zu erwähnen sorry) und wie Roland schon sagte, ist das Ergebnis 110101110. Hier muss man nochmal 01100110 (2x die 6) dazu addieren und das Ergebnis ist dann dieses 1 0100 0010.
Dann füge ich 3 Nullen hinzu 0001 0100 0010 und lese es ab (BCD!)