Aufgabe:
Es sei V ein K-Vektorraum und v1, v2, . . . , vn ∈ V seien linear unabhängig. Zeigen Sie, dass dann die folgenden Vektoren linear unabhängig sind:
(a) v1, v1 + v2, v1 + v3, . . . , v1 + vn für ein n ∈ N
Problem/Ansatz: Im folgenden findet ihr meinen Lösungsweg. Ist der so richtig oder ist dort irgendwo ein Denkfehler. Kommt mir nämlich zu einfach vor. Oder habe ich was vergessen?
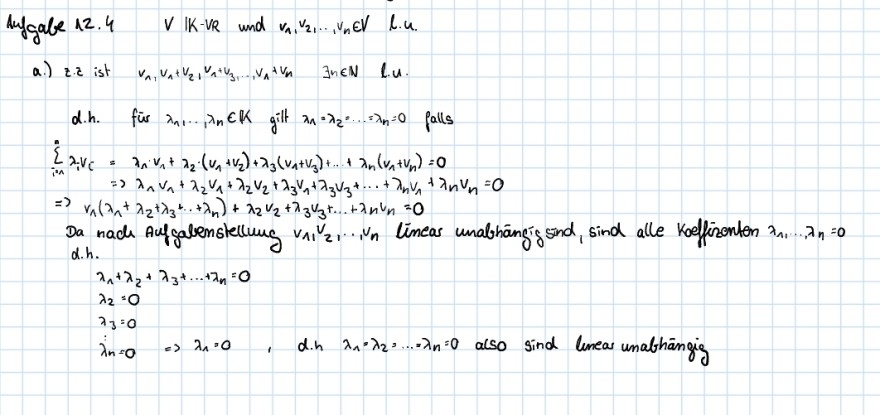
Text erkannt:
Augale 12.4 \( V \mid K-v_{R} \) und \( v_{1}, v_{2}, \ldots, v_{n} \in V \quad \) l.u.
a.) z.z ist \( v_{n}, v_{n}+v_{2}, v_{n}+v_{3}, \ldots, v_{A}+v_{n} \quad 3 n \in \mathbb{N} \quad \) l.u.
d.h. füs \( \lambda_{n}, \ldots, \lambda_{n} \in \mathbb{K} \) gilt \( \lambda_{n}=\lambda_{2}=\ldots=\lambda_{n}=0 \) falls
\( \begin{array}{l} \sum \limits_{i=1} \lambda_{i} v_{c}=\lambda_{n} \cdot v_{1}+\lambda_{2} \cdot\left(v_{1}+v_{2}\right)+\lambda_{3}\left(v_{1}+v_{3}\right)+\ldots+\lambda_{n}\left(v_{n}+v_{n}\right)=0 \\ \Rightarrow \lambda_{n} v_{n}+\lambda_{2} v_{1}+\lambda_{2} v_{2}+\lambda_{3} v_{1}+\lambda_{3} v_{3}+\ldots+\lambda_{n} v_{1}+\lambda_{n} v_{n}=0 \\ \Rightarrow v_{1}\left(\lambda_{n}+\lambda_{2}+\lambda_{3}+\ldots+\lambda_{n}\right)+\lambda_{2} v_{2}+\lambda_{3} v_{3}+\ldots+\lambda_{n} v_{n}=0 \end{array} \)
Da nach Aufgabenstellung \( v_{1}, v_{2}, \ldots, v_{n} \) linear unabhängigsind, sind alle koeffirenten \( \lambda_{1}, \ldots, \lambda_{n}=0 \) d.h.
\( \begin{array}{l} \lambda_{n}+\lambda_{2}+\lambda_{3}+\ldots+\lambda_{n}=0 \\ \lambda_{2}=0 \\ \lambda_{3}=0 \end{array} \)
\( \lambda_{n}=0 \Rightarrow \lambda_{1}=0 \), d.n \( \lambda_{1} \cdot \lambda_{2}, \ldots=\lambda_{n}=0 \) also sind lenear unathangig