Aufgabe:
Beim Vergleich zweier aufeinanderfolgender Landtagswahlen ergibt sich folgende prozentuale Wählerwanderung:
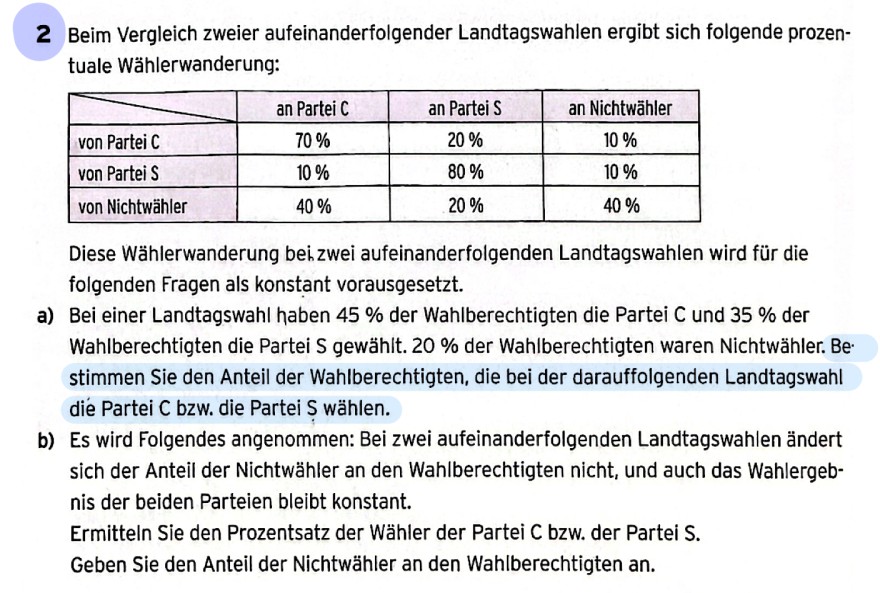
Diese Wählerwanderung bei zwei aufeinanderfolgenden Landtagswahlen wird für die folgenden Fragen als konstant vorausgesetzt.
a) Bei einer Landtagswahl haben \( 45 \% \) der Wahlberechtigten die Partei C und \( 35 \% \) der Wahlberechtigten die Partei S gewählt. 20 \% der Wahlberechtigten waren Nichtwähler. Be\( \cdot \) stimmen Sie den Anteil der Wahlberechtigten, die bei der darauffolgenden Landtagswahl die Partei C bzw. die Partei Ș wählen.
b) Es wird Folgendes angenommen: Bei zwei aufeinanderfolgenden Landtagswahlen ändert sich der Anteil der Nichtwähler an den Wahlberechtigten nicht, und auch das Wahlergebnis der beiden Parteien bleibt konstant. Ermitteln Sie den Prozentsatz der Wähler der Partei C bzw. der Partei S. Geben Sie den Anteil der Nichtwähler an den Wahlberechtigten an.
Problem/Ansatz:
 Text erkannt:
Text erkannt:
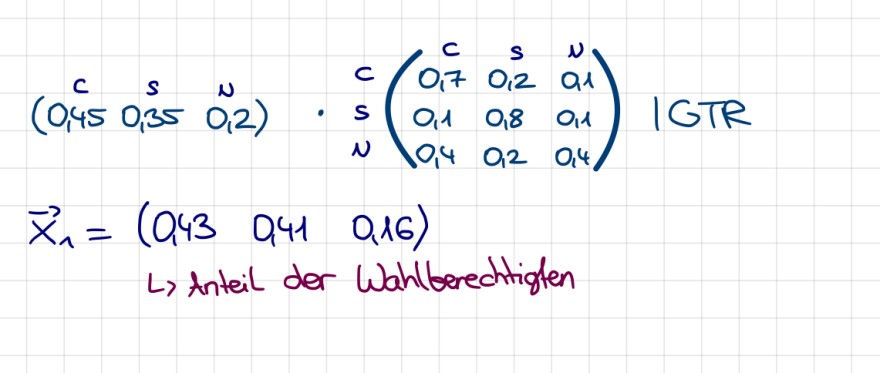
\( \begin{array}{l} \left(\begin{array}{ccc} c & s & n \\ 0,45 & 0,35 & 0,2 \end{array}\right) \cdot \quad \begin{array}{l} c \\ \end{array}\left(\begin{array}{ccc} c & s & N \\ 0,7 & 0,2 & 0,1 \\ 0,1 & 0,8 & 0,1 \\ 0,4 & 0,2 & 0,4 \end{array}\right) \text { | GTR } \\ \vec{x}_{1}=\left(\begin{array}{lll} 0,43 & 0,41 & 0,16 \end{array}\right) \\ \end{array} \)
Anteil der Wahlberechtigten
ist Nummer 2a.) richtig? und wie geht 2b?