Lotfußpunkt anders berechnen

Question

Das ist meine Aufgabe:

Text erkannt:

Hausaufgabe 13.3: Lotfußpunkt
Sei \( \vec{v}_{1}:=\left(\begin{array}{c}1 \\ 1 \\ 1 \\ 1\end{array}\right), \vec{v}_{2}:=\left(\begin{array}{c}1 \\ 0 \\ 1 \\ 4\end{array}\right), V:=\operatorname{Span}_{\mathbb{R}}\left(\vec{v}_{1}, \vec{v}_{2}\right) \) und \( \vec{w}:=\left(\begin{array}{c}3 \\ 1 \\ 5 \\ -5\end{array}\right) \in \mathbb{R}^{4} \).
(2 P.) Berechnen Sie den Lotfußpunkt \( L_{V}(\vec{w}) \).

Wie genau löst man das hier? Ich dachte immer, dass man bei der Lotfußpunktberechnung einen Punkt braucht und ich weiß auch nicht wirklich, was das mit dieser Spanweite und V bedeutet.

Comments

was das mit dieser Spanweite und V bedeutet

Flugzeuge und Vögel haben eine Spannweite, hier handelt es sich um den Unterraum V des ℝ^4, der von den Vektoren v1 und v2 aufgespannt wird :

Der Vektor f = α·v1 + β·v2 ist gesucht.

Answer 1

Aloha :)

Die beiden Vektoren \(\vec v_1\) und \(\vec v_2\) spannen eine Hyper-Ebene auf. Der Vektor \(\vec w\) liegt außerhalb dieser Hyper-Ebene. Daher gilt für alle \(a,b\in\mathbb R\):$$a\cdot\vec v_1+b\cdot\vec v_2\ne\vec w$$Wir addieren nun zum Vektor \(\vec w\) auf der rechten Seite einen Vektor \(\vec p\), sodass der Summenvektor \((\vec w+\vec p)\) in der Hyper-Ebene liegt. Dann gibt es \(a,b\in\mathbb R\) mit:$$a\cdot\vec v_1+b\cdot\vec v_2=\vec w+\vec p$$

Es existieren unendlich viele dieser Vektoren \(\vec p\). Wir suchen denjenigen Vektor \(\vec p\)$$\vec p=a\cdot\vec v_1+b\cdot\vec v_2-\vec w$$der zu den Basisvektoren \(\vec v_1\) und \(\vec v_2\) orthogonal ist:$$0\stackrel!=\vec v_1\cdot\vec p=a\cdot \vec v_1^2+b\cdot\vec v_1\cdot\vec v_2-\vec v_1\cdot\vec w=4a+6b-4$$$$0\stackrel!=\vec v_2\cdot\vec p=a\cdot \vec v_2\cdot\vec v_1+b\cdot\vec v_2^2-\vec v_2\cdot\vec w=6a+18b-(-12)$$

Das entstehende Gleichungssystem$$4a+6b=4\quad\land\quad6a+18b=-12$$wird gelöst durch:\(\quad a=4\;\land\;b=-2\)

Damit haben wir den Lotfußpunkt gefunden:$$\vec l=\vec w+\vec p=a\cdot\vec v_1+b\cdot\vec v_2=4\cdot\vec v_1-2\cdot\vec v_2=\begin{pmatrix}2\\4\\2\\-4\end{pmatrix}$$

Answer 2

Ich mal Dir mal ein 3D BIld von dem Thema (x4-abgeschnitten)

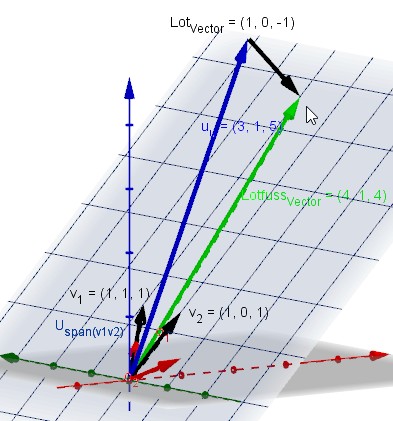
Der Lotfußvektor ist die orthogonale Projektion von w (u) auf die Ebene span(v1,v2). Es kommt jetzt darauf an, was Du als Handwerkszeug parat hast?

ONB bauen oder

\(\small Least-Squares \quad \min _{x}\|A x-b\|_{2}^{2}\)

\(\small \left(\begin{array}{rr}1&1\\1&0\\1&1\\1&4\\ \end{array}\right) \left(\begin{array}{r}x1\\x2\\x3\\x4 \end{array}\right) = \left(\begin{array}{r}3 \\ 1 \\ 5 \\ -5 \\ \end{array}\right)\)

\(\small  \left(A^{T} A x\right)_{i}=\left(A^{T} b\right)_{i} \\ \sum \limits_{k=1}^{m} a_{k, i} \sum \limits_{j=1}^{n} a_{k, j} x_{j}=\sum \limits_{k=1}^{m} a_{k, i} b_{k}\)