Flächenberechnung eines Oktaeders

Question

Meine Frage:
Ich brauche Hilfe, denn ich weiß nicht ob meine Lösung richtig ist!
Also die Aufgabe lautet:
Bestimme das Volumen eines oktaeders (= 2 auseinandergesetzte Pyramiden) mit der kantenlänge 1,75cm.

Meine Ideen:
Formel zur Volumenbestimmung einer Pyramide:
V = 2 x 1/3 G x h
das ganze mal zwei, weil ein oktaede aus 2 Pyramiden besteht also erstmal die Grundfläche ausrechnen:
G Pyramide = 1,75 cm x 1,75cm G = 3, 0625 cm²

Jetzt das Volumen:
Also: V eines Oktaeders = 2 x 1/3 x 3,0625 cm² x 1,75 cm
V = 3, 22 cm³

ist das so richtig?

Comments

Dei Gedankengang scheint mir logisch und richtig!

Answer 1

Wie oben zu lesen, setzt du die Höhe bei der Pyramidengleichung mit 1,75 cm ein, was leider nicht korrekt ist:

V = 2 * 1/3 * 3,0625 cm² * 1,75 cm

Denn du hast nur die Kantenlänge mit 1,75 cm gegeben. Die Höhe ist jedoch keine Außenkante! Die Höhe berechnest du über den Satz des Pythagoras.

Weshalb nutzt du nicht direkt die Volumenformel für Oktaeder:

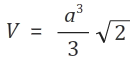
a ist die Kantenlänge.

Dann einfach einsetzen und sich wohlfühlen :)

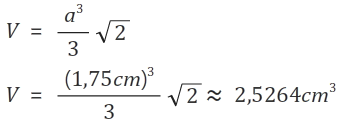
Berechnung mit Pyramidenvolumen

Wenn du das Oktaeder-Volumen wirklich über die beiden Pyramiden berechnen möchtest, dann geht das wie folgt (wie gesagt, musst du hierzu den Satz des Pythagoras kennen).

Hinweis: Wir brauchen das Dreieck mit den Seiten: Halbe-Diagonale (s/2), Höhe (h) und Außenkante (a), die zur Spitze geht. Siehe Abbildung:

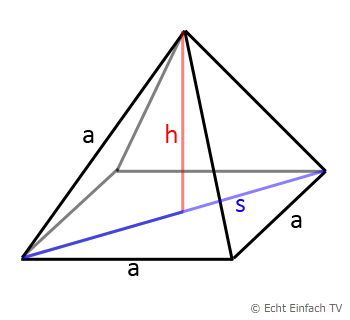
1. Seite s berechnen (Diagonale der Grundfläche):
a² + a² = s²
s² = a² + a²
s² = 1,75² + 1,75²
s² = 6,125
s = √6,125 = 2,47487 cm

2. Halbe Diagonale:

s/2 = 2,47487 cm/2 = 1,237437 cm

3. Höhe jetzt ausrechnen über Pythagoras:

h² = a² - (s/2)²
h² = (1,75)² - (1,237437)²
h² = 1,531249671031
h = √1,531249671031
h ≈ 1,2374 cm

4. Jetzt das Volumen einer Pyramide:

V_P = 1/3*G*h
V_P = 1/3*(1,75² cm²)*1,2374 cm
V_P ≈ 1,26318 cm³

5. Das Volumen des Oktaeders (zweimal das Volumen der Pyramide):

V_ges = 2*V_P
V_ges ≈ 2,5264 cm³