Aufgabe:
Bestimme die Gleichung der Ebene, welche durch den Punkt P1 = (3, 6, 4) geht und parallel zur xz-Ebene liegt.
Problem/Ansatz:
Hallo, ich habe mich gerade selber verwirrt, als ich mir vorstellen wollte, was die xz-Ebene ist.
Man muss ja die Ebenengleichung aufstellen also E:x = \( \begin{pmatrix} 3\\6\\4 \end{pmatrix} \) + r • Richtungsvektor + s • Richtungsvektor.
Das war meine Skizze, wie ich es mir vorgestellt habe:
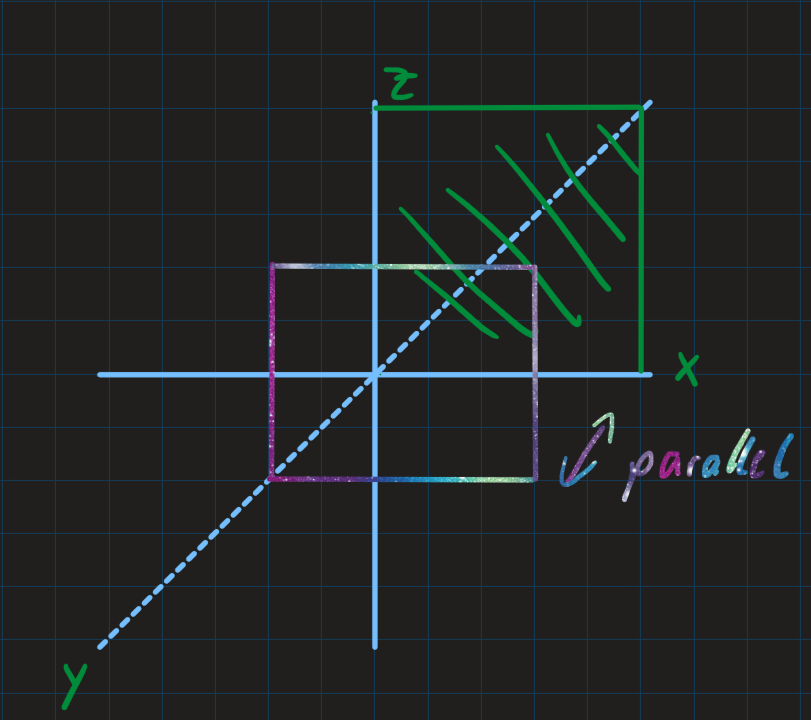
Wie wähle ich nun die Richtungsvektoren? Einer wäre doch \( \begin{pmatrix} 0\\1\\0 \end{pmatrix} \) oder? Was gibt es noch für Möglichkeiten?