Du darfst in Ungleichungssystemen keine Ungleichungen voneinander subtrahieren. Ein Beispiel:
(1) 7<10
(2) 5< 9
Beide Ungleichungen gelten. Die Differenz (1)-(2) wäre
7-5 < 10-9, was allerdings nicht stimmt.
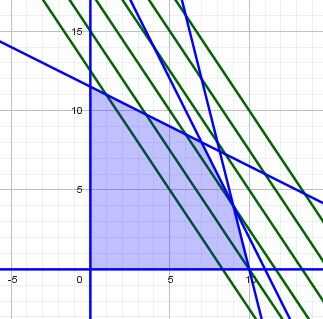
In der Abbildung siehst du das durch die Nebenbedingungen eingegrenzte Gebiet
sowie einige Gerade der Schar 3x+2y=c (von innen nach außen für c=25, c=30, c=35, ...)
Je weiter die Geraden nach außen wandern, um so kleiner ist der Bereich der Gerade, der sich im Gebiet befindet. Wenn c zu groß wird, liegen die Geraden komplett außerhalb.
Wenn man eine solche Gerade parallel verschiebt, ist die Ecke (7|8) der letzte Punkt des Gebiets, der gerade noch von einer Gerade der Schar getroffen wird.