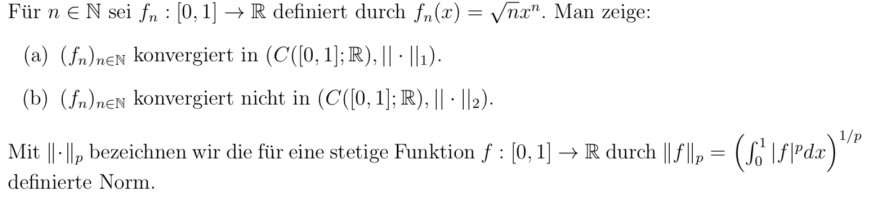
Text erkannt:
Für \( n \in \mathbb{N} \) sei \( f_{n}:[0,1] \rightarrow \mathbb{R} \) definiert durch \( f_{n}(x)=\sqrt{n} x^{n} \). Man zeige:
(a) \( \left(f_{n}\right)_{n \in \mathbb{N}} \) konvergiert in \( \left(C([0,1] ; \mathbb{R}),\|\cdot\|_{1}\right) \).
(b) \( \left(f_{n}\right)_{n \in \mathbb{N}} \) konvergiert nicht in \( \left(C([0,1] ; \mathbb{R}),\|\cdot\|_{2}\right) \).
Mit \( \|\cdot\|_{p} \) bezeichnen wir die für eine stetige Funktion \( f:[0,1] \rightarrow \mathbb{R} \) durch \( \|f\|_{p}=\left(\int \limits_{0}^{1}|f|^{p} d x\right)^{1 / p} \) definierte Norm.