Aufgabe:
weiterführende Berechnungen zum 2-D Sehbereich eines Menschen
Problem/Ansatz:
Sehbereich Mensch, gleiches Sehvolumen bei 2-D und 3-D
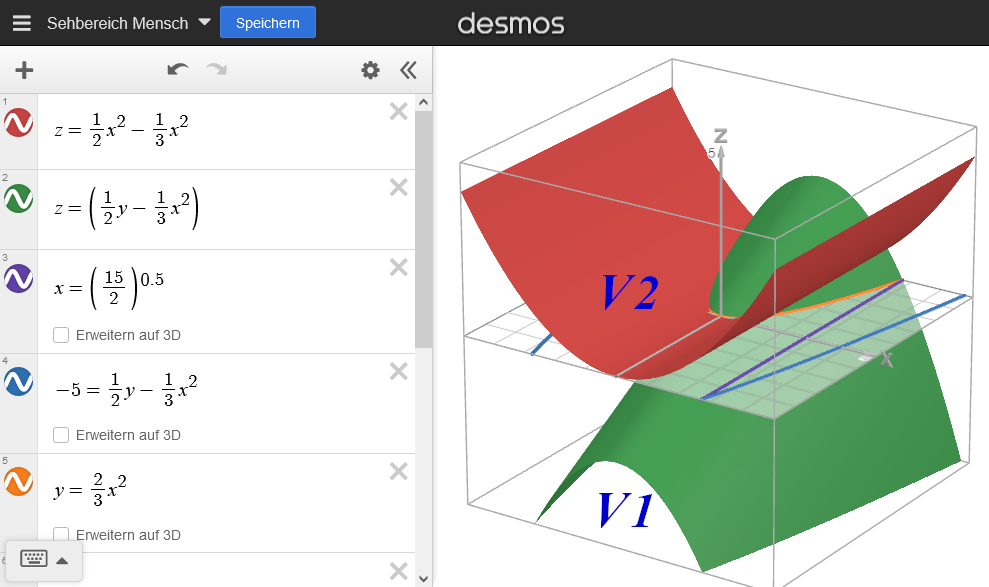
3-D Sehbereich: z=1/2y-1/3x^2 V1
2-D Sehbereich: y=x^2 z=1/2x^2-1/3x^2=1/6x^2 V2
Berechnung Sehvolumen 2-D, V2:
Integral von 0 bis 5 (1/6x^2) dx=6,944
6,944*2*(yA+yB)=6,944*2*(5+5)=138,88
z=1/6x^2 x=5 z=4,166
Vges.=(xA+xB)*(yA+yB)*4,166=416,66
V2=416,66-138,88=277,77
Berechnung Sehvolumen 3-D, V1:
z=1/2y-1/3x^2 z=-5 y=2/3x^2-10
y1=-5 x1=(15/2)^0.5
y2=0 x2=(15)^0.5
y3=5 x3=3*(5/2)^0.5
zO=f(x=0; y=5) zO=5/2
zU=f(x=0; y=-5) zU=-5/2
z=0 y=2/3x^2
Volumenberechnung 3-D:
Einteilung in 6 Bereich=2*3Bereiche
1. Integral von (15/2)^0.5 bis (15)^0.5 Integral von -5 bis 0 (1/2y-1/3x^2) dydx=-27,954
2. Integral von 0 bis 5 Integral von (15)^0.5 bis 3*(5/2)^0.5 (1/2y-1/3x^2) dxdy=-21,577
3. Integral von 0 bis 5 Integral von 0 bis (15/2)^0.5 (1/2y-1/3x^2) dxdy=5,7054
Addition der Teilvolumina:
27,954+21,577+5,7054=55,237 |*2 =110,474
Integral von (15/2)^0.5 bis (15)^0.5 (2/3x^2-10) dx=2,998
Integral von (15)^0.5 bis 3*(5/2)^0.5 (2/3x^2-10) dx=2,10
5*(15/2)^0.5+2,998=16,691
5*3*(5/2)^0.5-2,10= 21,617
16,691+21,617=38,308 |*2 =76,61 |*5 =383,08
383,08-110,474= 272,576
Vergleiche: 272,576 ist rund 277,7
den Fehler führe ich auf ein ungenaues Rechnen mit dem Integralrechner zurück......, auch wenn der Fehlerwert relativ groß ist
Berechnung Näherungsweise als Trapezprisma:
(15)^0.5*2*5*10=387,2983, ist etwas genauer
387,2983-110,474=276,8243 (!!!!)
es kann gesagt werden, daß 2-D und 3-D beim Menschen das gleiche Sehvolumen haben, aber eine andere Form...
eine zweimalige Integration von 1-D zu 3-D liefert das 3-D Sehvolumen
vergleiche diese zweimalige Integration mit der Energiebilanz, bzw. dem Leistungspotential eines Menschen...
wenn das Auge bei 2-D und 3-D gleich funktionieren würde, wäre auch 4-D, usw., möglich.....
Berechnung der Auflösungen des Auges bei y=5 bzw. y=-5:
z=1/2y-1/3x^2
1. y=5 z=5/2-1/3x^2
Integral von 0 bis (15/2)^0.5 (5/2-1/3x^2) dx=4,56435 |*2 =9,1287
Integral von (15/2)^0.5 bis 3*(5/2)^0.5 (5/2-1/3x^2) dx=-4,56435
5*3*(5/2)^0.5=23,717 |-4,56435 =19,152 |*2 =38,305
38,305+9,1287=47,4337
2. y=-5 z=-5/2-1/3x^2
5*(15/2)^0.5-9,1287=4,564354 |*2 =9,1287
47,4337/9,1287=5,19615
Näherung linear:
z-Richtung: 7,5/2,5=3 x-Richtung: 3*(5/2)^0.5/(15/2)^0.5=1,732
3*1,732=5,19615
abschließende Beurteilung:
Die Auflösungen wurden richtig berechnet, siehe Ergebnisse....!
Bei der Berechnung des 3-D Volumens ist mir auf Grund der anschließenden Differenz zum 2-D Volumen ein Fehler unterlaufen, ich weiß trotz mehrmaliger sorgfältiger Prüfung der Integrale bzw. Ihrer eingesetzten Grenzen nicht, wo Dieser zu suchen ist. Die Berechnungen mit dem angenäherten Trapezprisma war ja schon genauer...... Vielleicht lag es ja doch am Integralrechner, wie von mir vermutet. Sollte Jemanden der Fehler auffallen, dann wäre es schön, wenn man mich, Kontaktformular auf meiner Website, benachrichtigen würde! Im Voraus ein "Dankeschön"!

Text erkannt:
Sehbereich Mensch
Speichern
desmos
\( z=\frac{1}{2} x^{2}-\frac{1}{3} x^{2} \)
Dz \( \quad=\left(\frac{1}{2} y-\frac{1}{3} x^{2}\right) \)
( \( x=\left(\frac{15}{2}\right)^{0.5} \)
Erweitern auf 3D
\( -5=\frac{1}{2} y-\frac{1}{3} x^{2} \)
Erweitern auf 3D
\( y=\frac{2}{3} x^{2} \)
Erweitern auf 3D