Aufgabe:
Wir betrachten die Oberfläche der Einheitskugel im euklidischen Dreiraum. Als „Punkt“
bezeichnen wir ein Paar von antipodalen Punkten, als „Gerade“ eine Großkreis auf der
Kugel. Finden Sie mit Hilfe von GeoGebra experimentell heraus, ob der Satz von Pappos in
diesem Zusammenhang gilt.
Problem/Ansatz:
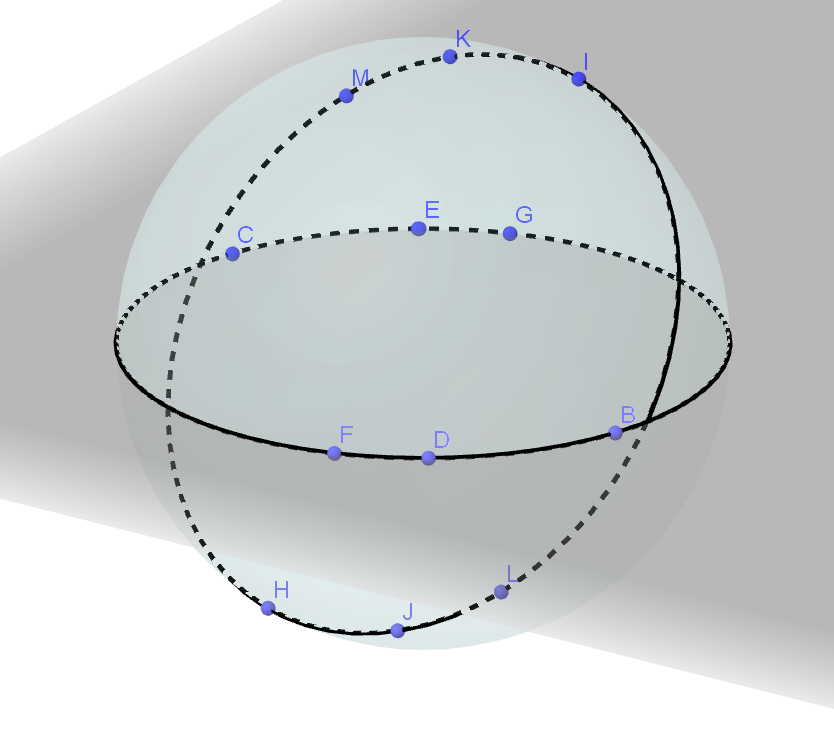
Ich habe soweit die zwei "Geraden", also zwei Großkreise, mit jeweils 3 "Punkten", also 3 antipodale Punktpaare, in Geogebra eingezeichnet.
Jetzt weiß ich aber nicht, wie ich die Punkte bzw. Punktpaare miteinander verbinden soll, da ein "Punkt" ja in diesem Fall zwei Punkte hat. (Anbei die Geogebra Grafik zu der Aufgabe)