Bestimmen Sie den Abstand des Punktes D von der Geraden, die durch die zwei Punkte

Question

Aufgabe:

Das Viereck ABCD bildet eine Raute R. Der Punkt A hat die Koordinaten (1,−1, 1), der
Punkt B - (−1, 3, 2). Der Punkt C mit der Koordinaten (β, 1, γ), β, γ ∈ IR liegt in der
yz−Ebene.
a) Geben Sie die Koordinaten von C und D an.
b) Bestimmen Sie den Abstand des Punktes D von der Geraden, die durch die zwei Punkte
A und B verläuft.
c) Durch eine Parallelverschiebung entsteht aus R eine Kopie R′. Die Verschiebung ist
derart, dass der Eckpunkt A von R in den Eckpunkt A′(−1, 1,−1) von R′ übergeht. Die
Punkte B, C, D gehen sinngemäß in die Punkte B′, C′, D′ über. Die bezeichneten
acht Punkte bilden die Ecken eines Spats S. Berechnen Sie das Volumen des Spates S.

Problem/Ansatz:

Wie löse ich diese Aufgabe?

Comments

Ergänze bitte, an welchem Teilproblem du scheiterst.

---

ganz am Anfang mir fehlt die Überlegung was ich rechnen muss

---

Du kannst die Koordinaten von \(C\) bestimmen mit \( \overline{AB} = \overline{BC}\) (weil Raute) und \( \beta = 0 \) (weil yz-Ebene).

Answer 1

Berechne die Länge von \( \vec{AB} \). Berücksichtige \( \beta = 0 \) (weil yz-Ebene).

Berechne die Länge von \( \vec{BC} \) in Abhängigkeit von γ. Diese Längen müssen gleich sein. So ergibt sich schließlich eine quadratische Gleichung mit zwei Lösungen für γ. Eine davon ist der gesucht Wert für γ.

Answer 2

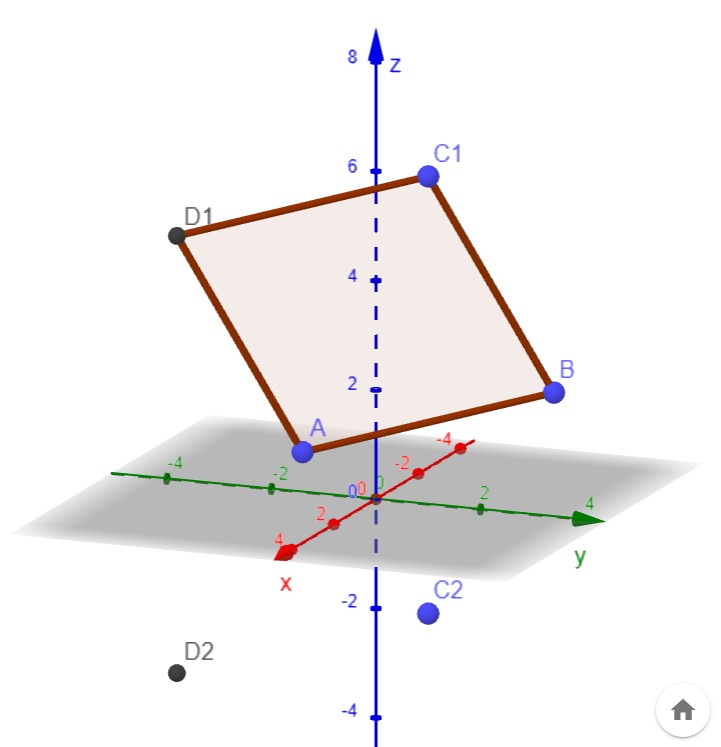
a) Geben Sie die Koordinaten von C und D an.

C mit der Koordinaten (β, 1, γ), β, γ ∈ IR liegt in der yz−Ebene.

Wenn C in der yz-Ebene liegt muss die x-Koordinate 0 sein. Also C(0, 1, γ)

Weiterhin ist ABCD eine Raute und damit alle Seiten gleich lang

|AB| = |BC|
|[-1, 3, 2] - [1, -1, 1]| = |[0, 1, γ] - [-1, 3, 2]| --> γ = 6 ∨ γ = -2

C1 = [0, 1, 6] ; C2 = [0, 1, -2]. Hier ist vermutlich C1 gemeint, da es im Koordinatensystem dann gegen den Uhrzeigersinn beschriftet wäre.

Da das Viereck weiterhin eine Raute und damit ein spezielles Parallelogramm ist gilt weiterhin, dass gegenüberliegende Seiten parallel sind.

D1 = A + BC1 =  [2, -3, 5]
D2 = A + BC2 =  [2, -3, -3]

Skizze