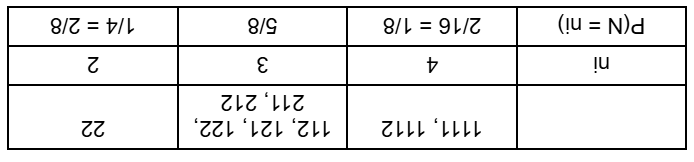
Nach Drehen des abgebildeten Glücksrads erhält man den Betrag ausgezahlt, der am Rand des ausgewählten Sektors steht. Das Glücksrad wird so oft gedreht, bis die Summe der ausgezahlten Beträge mindestens 4 € beträgt. N ist die Anzahl der dazu nötigen Drehungen. Berechne E(N) und V(N)!
Erwartungswert
E(N) = 4·1/8 + 3·5/8 + 2·2/8 = 23/8 = 2.875
Varianz
V(N) = (4 - 2.875)^2·1/8 + (3 - 2.875)^2·5/8 + (2 - 2.875)^2·2/8 = 23/64 ≈ 0.3594