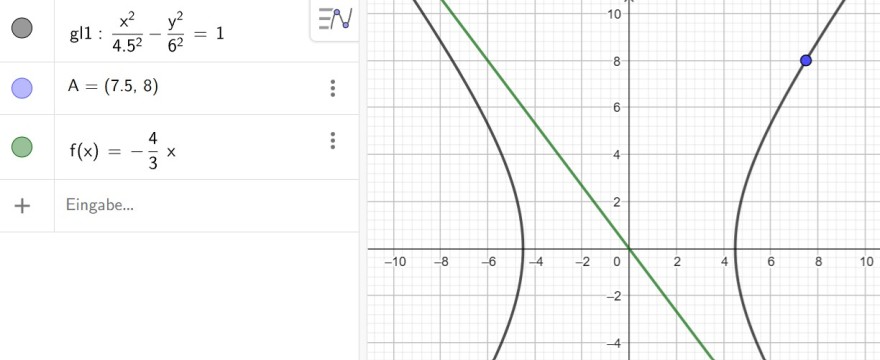
Du sollst auch nicht 4 und 3 für a und b einsetzen.
Der Quotient b/a hat den Wert 4/3
b/a = 4/3 → a = 3/4·b
Du kannst das Gleichungssystem mit dem Einsetzungsverfahren lösen.
Ich hätte aber vermutlich erst die eine Gleichung quadriert
a = 3/4·b
a² = 9/16·b²
Jetzt also in die erste Gleichung einsetzen und Auflösen.
Skizze