Rotationsvolumen Integral

Question

möchte von der Funktion: fx = 1/24x^4-1/6x^2+1 das Volumen bestimmen. Aber der Körper rotiert ja um die y-Achse und ich bekomme die Umkehrfunktion nicht auf die Reihe.

Vielleicht könnt ihr mir helfen.

Comments

Umkehrfunktion ?

In der Regel x mit y vertauschen und nach y auflösen

---

Es gibt noch eine zweite Formel dafür ohne die Umkehrfunktion: Vgl. hier:

https://de.wikipedia.org/wiki/Rotationskörper#Rotation_um_y-Achse

Answer 1

fx = 1/24x⁴-1/6x²+1

Ich nehme an du meinst

f ( x ) = 1/24 * x⁴ - 1/6 * x² + 1

Zur Bildung der Umkehrumfunktion
vertausche ich x und y und stelle nach y um
y = 1/24 * x⁴ - 1/6 * x² + 1
Umkehrfunktion
x = 1/24 * y⁴ - 1/6 * y² + 1 
1/24 * y⁴ - 1/6 * y² + 1 = x  |  * 24
y^4 - 4 * y^2 + 24 = 24 * x
Jetzt empfiehlt sich das ersetzen von
y^2 = z
z^2 - 4 * z = 24 * x  - 24
| lösbar mit quadratischer Ergänzung oder pq-Formel
z^2 - 4 * z + (2)^2 = 24 * x  - 24 + 4
( z - 2 )^2 = 24 * x - 20  | Wurzelziehen
z - 2 = ± √ ( 24 * x - 20 )
z :=  ± √ ( 24 * x - 20 ) + 2
z =  2 ± √ ( 24 * x - 20 )
Zurückersetzen
z = y^2
y^2 =  2 ± √ ( 24 * x - 20 )
y = ± √  [  2 ± √ ( 24 * x - 20 ) ]

Dies ist die Umkehrfunktion. Der negative
Funktionswert kann entfallen und es bleiben
2 Funktionen

y = √  [  2 + √ ( 24 * x - 20 ) ]
y = √  [  2 - √ ( 24 * x - 20 ) ]

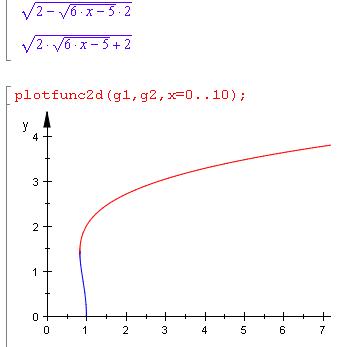
Hier der Graph der beiden Funktion
( blau ist die obere Funktion )

a

Da keine Integrationsgrenzen genannt sind kann auch
kein konkretes Volumen berechnet werden.

Von der blauen Kurve könnte man die Integrationsgrenzen
berechnen.
Stammfunktion
g ( x ) = √  [  2 - √ ( 24 * x - 20 ) ]
A ( x ) = [ g ( x ])^2 * π
A ( x ) =  [ 2 - √ ( 24 * x - 20 ) ] * π
V ( x ) = π * ∫  2 - √ ( 24 * x - 20 )  dx
V ( x ) = π * ∫  2 - ( 24 * x - 20 )^{1/2}  dx
V ( x ) = π * ( 2 * x - )
Stammfunktion
V ( x ) = π * ( 2 * x - 1/36 * ( 24 * x - 20 )^{3/2} )

Bei Fehlern oder Fragen wieder melden.

mfg Georg
 

 

Comments

Ja, das sieht sehr gut aus Georg. Danke für die Hilfe. Das ist quasi eine Obstschale oder Salatschüssel.

Die Grenzen kann ich mir ja selber aussuchen.

Bin jetzt wieder einen Schritt weiter.


Gibt es eigentlich ein Verfahren, womit ich diese Funktion leichter quadrieren kann, wie z.B. Hornerschema? Das ist ja immer ein riesiger Aufwand, müsste es mal mit Excel versuchen.

Für ein Volumen muss ich die Funktion quadrieren und dann das Integral ziehen.


Gruss aus Köln

---

Wenn du nicht gerade in einer Klausur sitzt sondern vor
einem PC kannst du arbeitsaufwendige Berechnungen
auch vom PC erledigen lassen.

Oben rechts auf dieser Seite findest du
Mathe-Tools - weitere - WolframAlpha - Tool aufrufen
und gibt es dann ein
expand ( 1/24 * x⁴ - 1/6 * x² + 1 )^2

Bin gern weiter behilflich.

mfg Georg
 

---

Okay. Wolfram Alpha kenne ich. Versuche es über die Feiertage mal mit Excel.

Als nächstes möchte ich das Integral fx= √x/x^2+1 lösen. Ach so, es handelt sich wider um eine Volumenfunktion, aus diesem Grunde wird die Funktion quadriert und der Wurzelausdruck fällt weg, so weit bin ich schon mal:) Im Nenner habe ich jetzt wieder ein Polynom. Ich versuche es mal bis Montag zu lösen, bitte erst dann die Lösung schicken.


Gruss aus Köln

---

Du hast sicherlich nicht genügend geklammert

f ( x ) = √ [ x / ( x²+1) ]

Besser ist es auch mit der Funktion eine neue Frage zu stellen.

 mfg Georg

---

Ja, mit den Klammern habe ich es nicht so. Nur das x hat die Wurzel, nicht der Term aus dem Nenner.

---

 

Probe durch differenzieren der gefundenen Funktion

Bei Fehlern oder Fragen wieder melden.

mfg Georg

---

Danke für die Lösung. An die Substitution habe ich jetzt nicht gedacht, war ja doch nicht so schwer.

Könnte ich auch den Zähler x einzeln durch den Nenner dividieren und integrieren? Also, ∫x/x^4 dx +∫x/2x dx +∫x/1 dx?


Gruss

---

Nö.

Du kannst ja einmal vergleichen ob
x / ( x^2 +1 )^2 =  x / x⁴ + x / 2x + x / 1

für z.B. x = 3 ist.

mfg Georg