Für welche a besitzt die quadratische Gleichung \(x^2+2a^2x+13a^2-36=0\) eine, zwei bzw. keine reelle Lösung?
Weg über die Ortskurve der Tiefpunkte
\(f_a(x)=x^2+2a^2x+13a^2-36\)
\(f'_a(x)=2x+2a^2\)
\(2x+2a^2=0\)
\(x=-a^2\)
\(f_a(-a^2)=a^4-2a^4+13a^2-36=-a^4+13a^2-36\)
\(o(x)=-x^2-13x-36 \)
An den Nullstellen von \(o \) hat die quadratische Gleichung eine Lösung.
\(x^2+13x+36=0 \)
\(x^2+13x=-36 \) quadratische Ergänzung und 1. Binom
\((x+6,5)^2=-36 +6,5^2= 6,25|±\sqrt{~~}\)
1.)
\(x+6,5= 2,5\)
\(x_1= -4\) mit \(x=-a^2\) → \(-4=-a^2\) → \( a_1,_2=±2 \)
2.)
\(x+6,5= -2,5\)
\(x_2= -9\) mit \(x=-a^2\) → \(-9=-a^2\) → \( a_1,_2=±3 \)
Zeichnungen für eine Lösung:
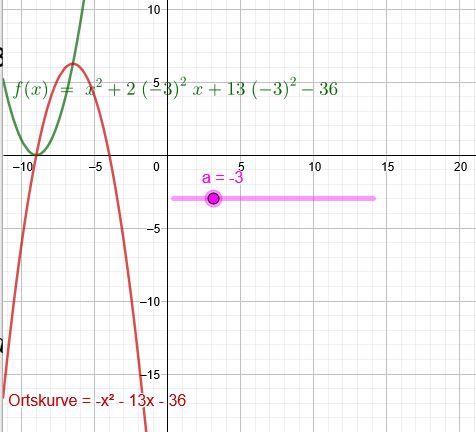
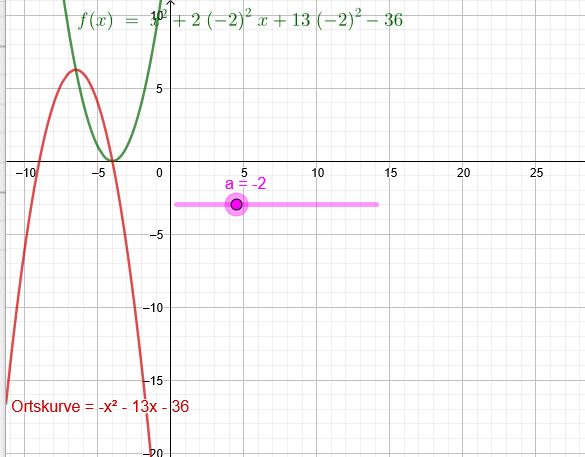
Da \(f_a\) eine nach oben geöffnete Parabel ist, hat sie im Bereich \(-3<a<-2\) oder \(2<a<3\) keine Nullstellen, weil das Maximum der Ortskurve \(o\) und das Minimum von \(f)\) im besagten Bereich oberhalb der x-Achse liegen.
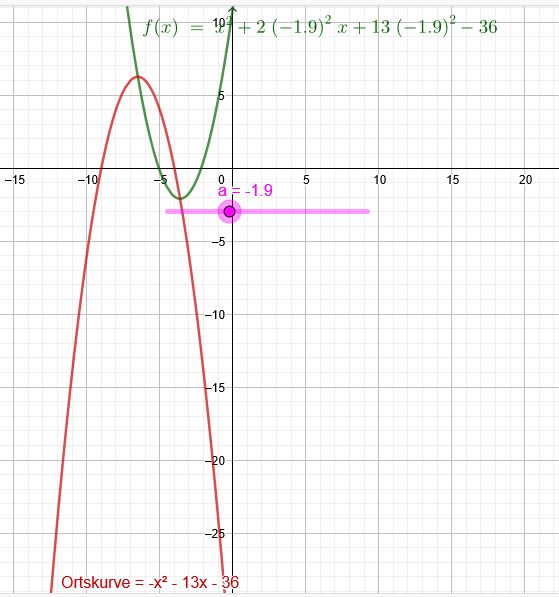
Zeichnungen für keine Nullstellen:
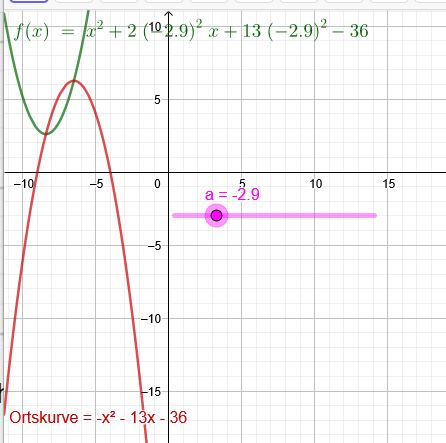
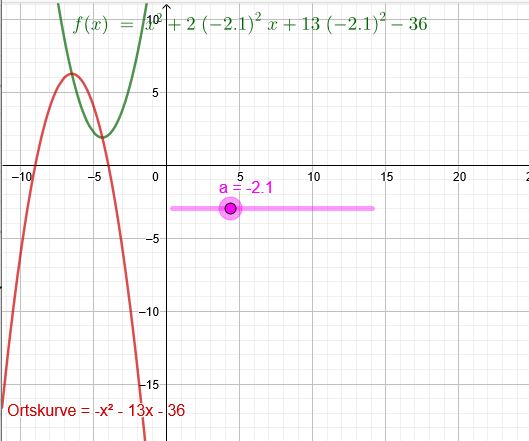
2 Nullstellen hat sie im Bereich \(a<-3\) oder \(-2<a<2\) oder \(a>3\)
Zeichnungen für 2 Nullstellen:
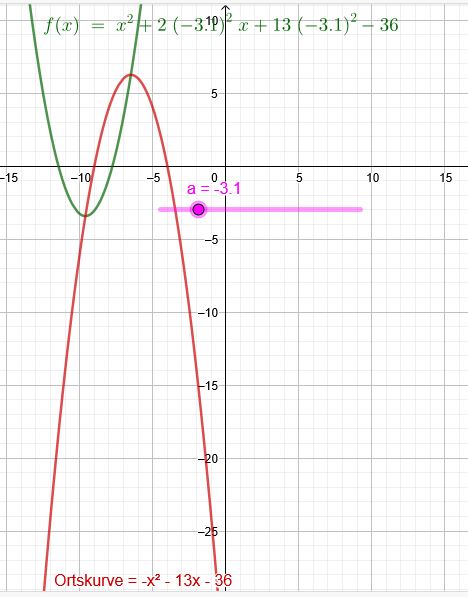
1.) Eine Lösung bei \( a_1,_2=±2 \) oder \( a_1,_2=±3 \)
2.) 2 Nullstellen hat sie im Bereich \(a<-3\) oder \(-2<a<2\) oder \(a>3\)
3.) Da \(f_a\) eine nach oben geöffnete Parabel ist, hat sie im Bereich \(-3<a<-2\) oder \(2<a<3\) keine Nullstellen, , weil das Maximum der Ortskurve \(o\) und das Minimum von \(f)\) im besagten Bereich oberhalb der x-Achse liegen.