Das ist eine Erklärung zur Aufgabe 3)
Fertig rechnen solltest du noch selbst.
f(x) = x^3 + x^2 - 5
g(x) = 4x - 5
Gleichsetzen um die Integrationsgrenzen zu bestimmen.
x^3 + x^2 -5 = 4x -5
x^3 + x^2 - 4x = 0
x(x^2 + x - 4) = 0
x1 = 0, x2,3 = 0.5 (-1 ±√(1+16)) = -0.5 ±0.5 √17
Es gibt also 2 solche Flächenstücke.
Die müssen separat berechnet werden.
Zuerst mit Integrationsgrennen -0.5 - 0.5√17 = -2.5616 und 0
Und dann zwischen 0 und -0.5 + 0.5√17 = 1.5616
Differenz d(x) = f(x) - g(x) = x^3 + x^2 - 4x
Stammfunktion D(x) = 1/4 x^4 + 1/3 x^3 - 2 x^2 + C
Jetzt noch die Grenzen einsetzen und die bestimmten Integrale berechnen. Zum Schluss den Betrag nehmen, falls etwas Negatives rauskommt.
eingeschlossenes Flächenstück links der y-Achse
F = | 1/4 *0^4 + 1/3 *0^3 - 2*0^2 - (1/4 *(-2.5616)^4 + 1/3*(-2.5616)^3 - 2*(-2.5616)^2 ) |
=| - (1/4 *(-2.5616)^4 + 1/3*(-2.5616)^3 - 2*(-2.5616)^2 ) | = 7.9622
eingeschlossenes Flächenstück rechts der y-Achse
F = | (1/4 *(1.5616)^4 + 1/3*(1.5616)^3 - 2*(1.5616)^2 ) - (1/4 *0^4 + 1/3 *0^3 - 2*0^2) |
= | (1/4 *(1.5616)^4 + 1/3*(1.5616)^3 - 2*(1.5616)^2 )| = 2.12113
Summe der beiden eingeschlossenen Flächeninhalte: 10.083
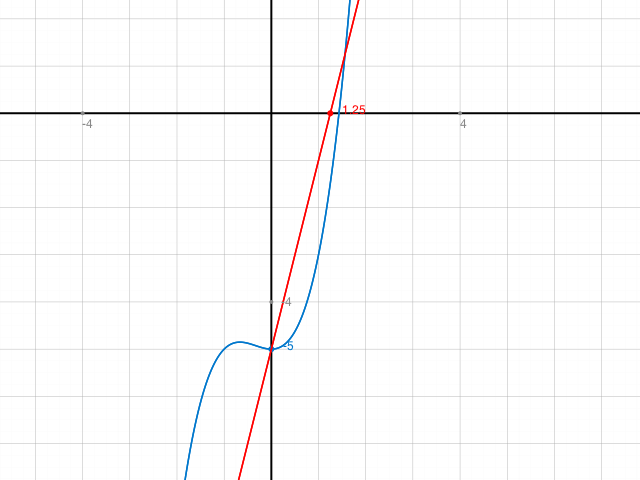
In der Skizze siehst du die beiden eingeschlossenen Flächenstücke (das Linke ist leider nicht ganz auf dem Ausschnitt:
2b) 5 schwarz, 3 rot, 2 grün Total 10 Stifte. ohne Zurücklegen.
i) Der 1. rot und der 2. grün
Zuerst 3 günstige (rot) und 10 mögliche (alle)
und dann noch
2 günstige (grün) und 9 mögliche (einer ist weg)
Produktregel:
P(i) = 3/10 * 2/9 = 1/15
ii) genau einer rot und einer grün
entweder:
[Zuerst 3 günstige (rot) und 10 mögliche (alle)
und dann noch
2 günstige (grün) und 9 mögliche (einer ist weg)]
oder
[Zuerst 2 günstige (grün) und 10 mögliche (alle)
und dann noch
3 günstige (rot) und 9 mögliche (einer ist weg)]
Produktregel und Additionsregel:
P(ii) = 3/10 * 2/9 + 2/10 *3/9 = 2/15
Anmerkung ist dasselbe wie 2 * 1/15. (Beide Reihenfolgen gleich wahrscheinlich)
iii) Genau einer grün
entspricht: 2* P(der erste ist grün und der zweite nicht grün)
Zuerst 2 günstige (grün) und 10 mögliche (alle)
und dann noch
8 günstige (nicht grün) und 9 mögliche (einer ist weg)
Produktregel:
P(iii) = 2*2/10 * 8/9 = 1/15
iv) beide schwarz
Zuerst 5 günstige (schwarz) und 10 mögliche (alle)
und dann noch
4 günstige (schwarz) und 9 mögliche (einer ist weg)
Produktregel:
P(iv) = 5/10 * 4/9 =2/9
v) beide nicht rot
Zuerst 7 günstige (nicht rot) und 10 mögliche (alle)
und dann noch
6 günstige (nicht rot) und 9 mögliche (einer ist weg)
Produktregel:
P(iv) = 7/10 * 6/9 =7/15