Aufgabe:
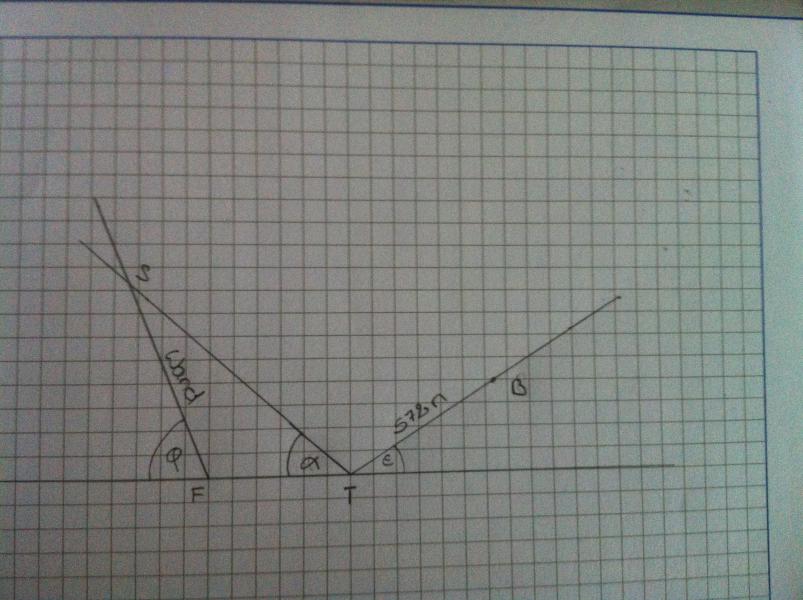
Eine \( 572 \mathrm{~m} \) lange Lifttrasse befindet sich auf einem unter \( \epsilon=32^{\circ} 14^{\prime} \) ansteigenden Schihang. Gegenüber des Schihanges befindet sich eine Felswand, deren mittlere Neigung \( \varphi=74^{\circ} 10^{\prime} \) beträgt. Die Talstation \( T \) des Liftes und der Fußpunkt \( F \) der Felswand befinden sich in derselben Horizontalebene! Von \( T \) aus erscheint der höchste Punkt \( S \) der Felswand unter einem Höhenwinkel \( \alpha=41^{\circ} 27^{\prime} \), von der Bergstation \( B \) aus erscheint \( S \) unter dem Höhenwinkel \( \beta=23^{\circ} 42^{\prime} . \) In halber Höhe der Wand befindet sich ein Bergsteiger. (Beachte: \( T, B, F \) und \( S \) liegen in einer Vertikalebene.)
a) Welcher Höhenunterschied besteht zwischen der Talstation \( T \) und dem höchsten Punkt \( S \) der Felswand?
b) Unter welchem Höhenunterschied erscheint der Bergsteiger von der Talstation \( T \) aus?
4. Gegeben sind die Funktionen \( f \) und \( g \) mit den Termdarstellungen
\( f(x)=\frac{x^{2}}{2}-x+1 \quad g(x)=\frac{1}{2} x^{3}-\frac{5}{2} x^{2}+\frac{1}{2} x+6 \)
Problem:
Ich bekomme keine Skizze aus den Angaben hin. Ausehen tut das ganze bei mir bis jetzt irgenwie so, wobei ich jetzt nicht weiß wie es weiter geht. T und F müssen in einer Horizontalebene liegen was sie ja auch tun aber gleichzeitig muss T,B,F und S in einer Vertikalebene liegen. Das rechnen selbst sollte kein Problem darstellen.