Fairer Münzwurf und Wurf mit einer Zinkmünze

Question

Aufgabe über Münzwahrscheinlichkeiten:

Sie verwenden faire Münzen.
(a) Nehmen Sie zwei Münzen und werfen Sie beide Münzen 10-mal. Zählen Sie jeweils die Anzahl von "Kopf" (es kommen also die Ereignisse 0, 1 und 2 mal "Kopf" vor). Tragen Sie Ihre Ergebnisse in ein normiertes Histogramm ein. Überlegen Sie sich nun, wie das normierte Histogramm für n Würfe (n sehr groß) aussähe und skizzieren Sie Ihre Idee.

(b) Für sehr große Wurfzahlen n, wie sähen die normierten Histogramme für 
- 1 Münze
- 3 Münzen
- 5 Münzen
aus?

(c) Zum Grübeln: Sie haben eine Münze. An der Münze ist irgendwas faul. Sie würden eigentlich erwarten, dass die Wahrscheinlichkeiten für Kopf Oder Zahl gleich groß sind. Das scheint bei dieser Münze aber nicht der Fall zu sein.  Wie können Sie mit zwei Würfen der gezinkten Münze einen Wurf einer fairen Münze simulieren?

Wie immer gibt es Lösungen, die noch kontrolliert werden müssen.

Hier sind meine Ergebnisse vom Münzwurf:

Münzexperiment

n	1	2	3	4	5	6	7	8	9	10
K	0	1	1	1	1	2	1	1	0	1

Einteilung in 3 Klassen: 0,1,2


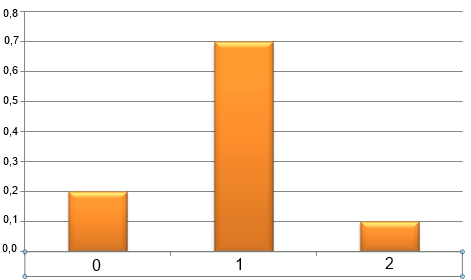
zu b)
Annahme 100 Würfe

1 Münze: Das Histogramm würde sich um die 0,5 (50%) einpegeln, da 1/2 Wahrscheinlichkeit. ±10%

3 Münzen: Das Histogramm würde sich nun ungleichmäßiger verteilen, da 1/2 mit 3 Münzen: 1/2³=0,125*3=37,5% Wahrscheinlichkeit. ±10%

5 Münzen: Das Histogramm würde sich nun noch ungleichmäßiger verteilen, da 1/2⁴=0,625*3=0,1875=18,75%

Je höher die Anzahl der Münzen, desto unregelmäßiger bzw. "ungenauer" werden die Histogramme.

Annahme, die falsch sein wird: Für höhere Werte könnte man die Gauß-Verteilung verwenden wie das Kugelexperiment (entweder links oder rechts).

Comments

Zinkmünze:

Mit einem fairen sechsseitigen Würfel zuerst eine 2 und dann eine 3 zu würfeln ist genauso wahrscheinlich, wie zuerst eine 3 und dann eine 2 zu würfeln. Unter Umständen kann man manche Wurfkombinationen ignorieren.

Vielleicht muss man die Münze runterfallen lassen, um den Versuch zu wiederholen damit man die andere Seite nach dem aufheben erhält, um dann beim erneuten Wurf eine faire Münze simuliert.

---

Korrektur bei 5 Münzen:

Das oben stehende Ergebnis trifft für 4 Münzen zu, hier ist die Korrektur:

5 Münzen: Das Histogramm würde sich nun noch ungleichmäßiger verteilen, da 1/2⁵=0,03125*3=0,09375=9,375% 

Answer 1

a)

 

Wahrscheinlichkeitsverteilung

k	0	1	2
P(X = k)	0.25	0.5	0.25

 

b)

 

1 Münze

k	0	1
P(X = k)	0.5	0.5

 

3 Münzen

k	0	1	2	3
P(X = k)	1/8	3/8	3/8	1/8

 

5 Münzen

k	0	1	2	3	4	5
P(X = k)	1/32	5/32	10/32	10/32	5/32	1/32

Comments

Also kann man allgemein für b) die Gaußverteilung verwenden. Bei a) hast du auch die allgemeine Gaußform verwendet. Bei meinen Münzwerten würden die Ergebnisse wie folgt lauten:

Münzexperiment

k	0	1	2
P(X = k)	0.2	0.7	0.1

Bei sehr vielen (n) Würfen würden sich die 3 Balkendiagramme wesentlich ändern und in etwa die Gaußwerte annehmen (0.25,0.5,0.25).

Was meinst du was es mit der Zinkmünze auf sich hat? Ist mein Zinkmünzenansatz richtig? Oder gibt es einen andere Möglichkeit?

---

Ich wüsste nur einen Ansatz

KZ wird wie Kopf gewertet und

ZK wird wie Zahl gewertet.

Dumm ist es wenn KK oder ZZ auftritt. Dann müsste leider nochmal geworfen werden.

---

Das ist ein sehr guter und vor allem eleganterer Ansatz, denn jedes Mal die Münze "versehentlich" fallen lassen und sich dann zu bücken, um die Münze aufzuheben macht nicht viel Sinn, außer dass man einige Kniebeugen macht und sich etwas trainiert ;) Vielen Dank für deine Unterstützung!