Ich habe auch mal eine Skizze gemacht:
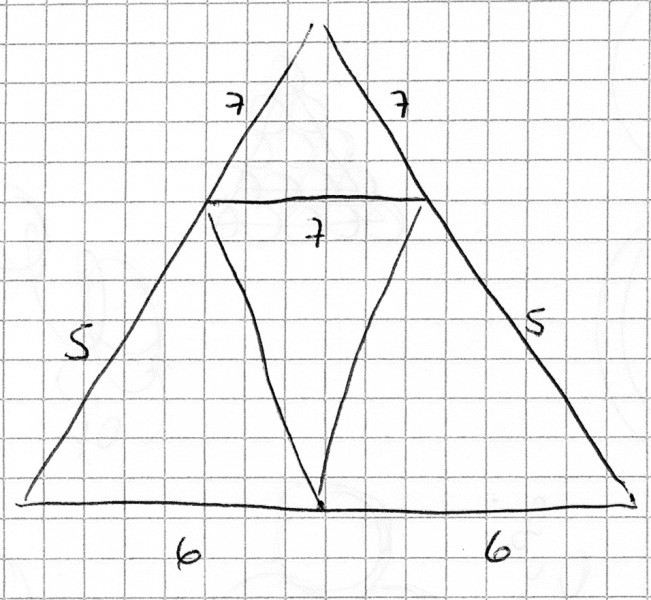
Die Höhe des linken unteren Dreiecks lässt sich jetzt mit dem Pythagoras bestimmen.
h = √(5^2 - (6 - 3.5)^2) = 5/2·√3
Das ist also auch die Höhe unseres mittigen Dreiecks. Damit lässt sich jetzt auch die Schenkellänge bestimmen.
s = √((5/2·√3)^2 + 3.5^2) = √31
Und auch die Fläche können wir über die Höhe recht einfach bestimmen
A = 1/2 * 7 * (5/2·√3) = 35/4·√3