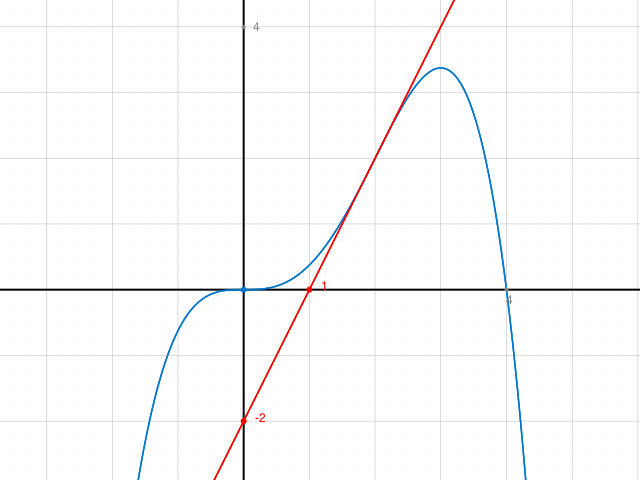
f(x) = 0.5x3 - 0.125 x4
f'(x) = 1.5 x^2 - 0.5x^3
a) f'(x) = 0 = 1.5 x^2 - 0.5x^3 = x^2 (1.5 - 0.5x)
x1,2 = 0, x3=3
y1,2 = 0, y3 = 3.375 = 27/8
Extrempunkt (3| 3.375)
Art?
f ''(x) = 3x - 1.5x^2
f ''(3) = 9 - 13.5 = -4.5
Relatives Maximum.
b) Wendepunkt…
f ''(x) = 3x - 1.5x^2 = 0 = x(3-1.5x)
x1 = 0 , x2 = 2
y1 = 0, y2 = 2
Wendepunkte
W1(0|0) und W2(2/2)
Wendetangenten
t1: y=0, da horizontale Tangente in W1.
t2:
Steigung. f'(2) = 2
y=2x+q durch W2
2 = 4 + q
-2=q
t2: y = 2x - 2
Kontrolle: Schaubild. Punkte und Tangenten noch selbst anschreiben.