f(x)=1/2*x+1/(2x), Extrempunkte und Wendepunkte, Stammfunktion, Flächen- und Volumenbestimmung

Question

f(x)=1/2*x+1/(2x)

 e) Extrempunkte berechnen und zeigen das Fkt. keine Wendepunkte hat
 g) Eine Stammfunktion bestimmen
 h) Flächenbestimmung die zwischen Graph von f seiner Asymptote und den Graden x=1 und x=4 begrennzt wird
 i) Volumenbestimmung wenn man den Körper um die x-Achse drehen würde im Intervalll (1;4)

Answer 1

0. Skizze: für f(x)=1/2*x+1/(2x)

 

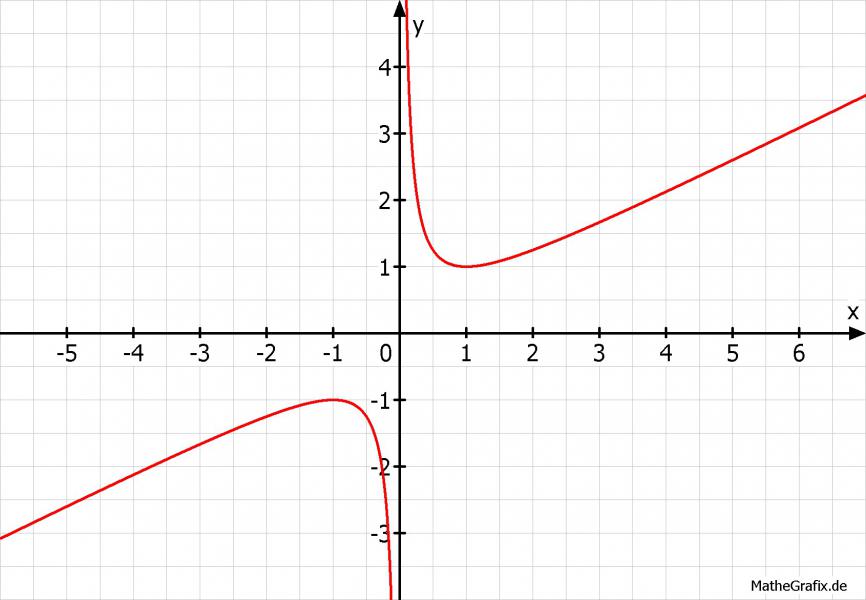
1. Bestimmung der Ableitungen:

x ∈ ℝ\{0}
f(x) = x/2 + 1/(2*x);
f'(x) = 1/2 - 1/(2*x^2);
f''(x) = 1/x^3;
f'''(x) = -3/x^4;

 

2. Bestimmung der Extrempunkte:

Ein Extrempunkt findet sich immer an einer Stelle an der die 1. Ableitung 0 wird, also bei einem x-Wert an dem die Funktion f(x) die Steigung 0 hat.

f'(x) = 1/2 - 1/(2*x^2) = 0;
x₁ = 1; in f(x) --> f(x₁) = 1;      EP₁(1 | 1);
x₂ = -1; in f(x) --> f(x₂) = -1;   EP₂(-1 | -1);

Um zu bestimmen ob es sich um ein Maximum oder ein Minimum handelt, setzt man die x-Werte noch in die 2. Ableitung ein (Alternative: Wetetabelle und auf Vorzeichenwechsel achten, hier nicht betrachtet, nur auf Wunsch)

EP₁(1 | 1); f''(x₁) = 1 > 0  --> Minimum
EP₂(-1 | -1); f''(x₂) = -1 < 0 --> Maximum

 

3. Wendepunkte:

Ob ein Wedepunkt vorliegt, prüft man mit dem
* Notwendigen Kriterium: f''(x) = 0;
und dem
* Hinreichenden Kriterium: f'''(x) =/= 0;

Setzt man nun f''(x) = 0 = 1/x³ so sieht man, dass es keine Lösung für diese Gleichung gibt. Es existiert also kein x, das die Gleichung erfüllt, bzw. das Multiplizieren mit x^3 führt zu einem Widerspruch.
Es existieren also keine Wendepunkte.

 

4. Stammfunktion:

F(x) = ln(x)/2 + x^{2/4} + c --nur eine Stammfunktion: c=0 --> F(x) = ln(x)/2 + x² /4;
(Für ausführliche Integration --> Kommentar).

 

5. Flächenbestimmung:

5.1 Fläche für 0 ≤ x ≤ 1:

F(x=1) - F(x=0) --> Funktioniert nicht, da der ln(0) nicht definiert ist.
Bin mir aber nicht 100% sicher ob das ausreicht.

5. Fläche für 1 ≤ x ≤ 4:

A = F(x=4) - F(x=1) ≈ 4,6931 - 0,25 ≈ 4,44;

 

6. Volumenbestimmung:

Bei der Rotation um die x-Achse gilt:
V = π*∫_a^b f²(x) dx;

F(x) = ∫ f²(x) dx = (x^4 + 6*x^2 - 3)/(12*x) + c;
V = F(x=4) - F(x=1) ≈ 21,79;

Comments

Ergänzung zu 5.1:
Skizze:

Für die Asymptote gilt: a(x) = x/2;
A(x) = x^2/4 + c;
FA = A(x=4) - A(x=1) =  3,75;
A ≈ 4,44; (aus 5.2, Fläche zwischn Graf und x-Achse von x=1 bis x=4)
A - FA = 4,44 - 3,75 = 0,69;