Ich interpretier mal so: das s(φ)=cosφ-sinφ mit φ∈[0,2π)bedeutet:
Auf einem um φ gegen die positive x-Achse gedrehten Leitstrahl ist der
entsprechende Punkt P genau cosφ-sinφ vom Nullpunkt entfernt.
Dann sieht das so aus
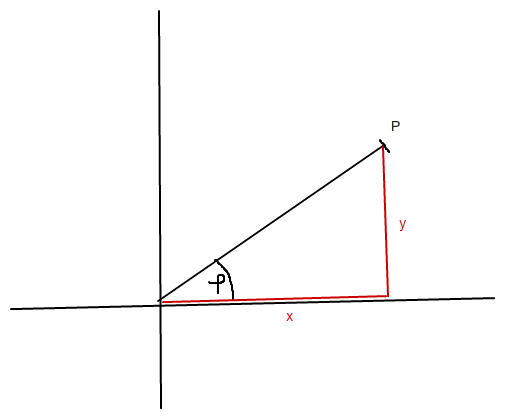
Und die Strecke OP hat die Länge r = cosφ-sinφ.
Und du willst eine Darstellung in der Form F(x,y) = 0.
Das wäre so (Pythagoras) r^2 = (cosφ-sinφ)^2 = x^2 + y^2
1 - 2 sin(φ)*cos (φ)= x^2 + y^2
außerdem hast du cos (φ)= x/r und sin (φ)= y / r einsetzen gibt
1 - 2 * x * y / r^2 = x^2 + y^2 |*r^2
r^2 - 2xy = r^4
-2xy = r^4 - r^2 = r^2 * ( r^2 - 1 )
0 = (x^2 + y^2 ) * ( x^2 + y^2 - 1 ) + 2xy
Dann wäre F(x,y) = (x^2 + y^2 ) * ( x^2 + y^2 - 1 ) + 2xy