Wie berechne ich den Flächeninhalt zwischen zwei Graphen?

Question

Ich stehe gerade ziemlich auf dem Schlauch... Ich wollte den Flächeninhalt, der von diesen beiden Funktionen eingeschlossen wird, berechnen.

y = x²

y = x + 2

Mit dem Ansatz ist mir alles klar (differenzfunktion, integrieren und pipapo...). Könnte vielleicht einer von Euch mir einen kompletten Rechenweg geben, damit ich meinen Fehler sehen kann?

Answer 1

Also an sich hast du ja eigentlich fast alles schon gesagt.

Als erstes musst du aber noch die Schnittpunkte der beiden Funktionen berechnen - dazwischen willst du den Flächeninhalt nämlich wissen!

Also musst du erstmal die Werte ausrechnen, für die x²=x+2 gilt:

x² = x+2  |-(x+2)

x²-x-2 = 0

Die pq-Formel liefert nun die Ergebnisse:

x_1/2 = 1/2 ± √(1/4 + 2)
x_1/2 = 1/2 ± √(9/4)

x_1/2 = 1/2 ± 3/2

x₁ = 2

x₂ = -1

Jetzt musst du noch wissen, welche der beiden Funktionen oberhalb verläuft und welche unterhalb, damit du die Differenzfunktion richtig bestimmst. Dafür bietet es sich an, die beiden Funktionen wenigstens grob zu skizzieren:

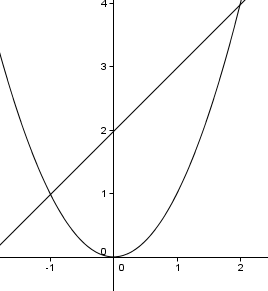
An sich ist es auch nicht so schlimm, wenn du diesen Schritt überspringst, solange dir klar ist, dass die Fläche zwischen zwei Funktionen immer positiv ist! Wenn also etwas negatives herauskommt, drehst du am Ende einfach das Vorzeichen um.

Hier ist nun also die lineare Funktion die obere, also lautet die Differenzfunktion:

g(x) = x + 2 - x²

Diese musst du jetzt in den Grenzen von -1 bis 2 integrieren, das ergibt den gesuchten Flächeninhalt A.

$$ \int _ { - 1 } ^ { 2 } \left( - x ^ { 2 } + x + 2 \right) d x = \left[ - \frac { x ^ { 3 } } { 3 } + \frac { x ^ { 2 } } { 2 } + 2 x \right] _ { - 1 } ^ { 2 } = \left( - \frac { 8 } { 3 } + \frac { 4 } { 2 } + 4 \right) - \left( - \frac { - 1 } { 3 } + \frac { 1 } { 2 } - 2 \right) $$ $$ \int _ { - 1 } ^ { 2 } \left( - x ^ { 2 } + x + 2 \right) d x = - \frac { 9 } { 3 } + 8 - \frac { 1 } { 2 } = \frac { 9 } { 2 } $$

Die Lösung lautet also:

A = 9/2

Answer 2

Wir bilden die Differenzfunktion

d(x) = x^2 - (x + 2) = x^2 - x - 2

Nun suchen wir hier die Nullstellen der Differenzfunktion d(x) = 0

x^2 - x - 2 | pq-Formel

x1 = -1 und x2 = 2

Nun berechne ich die Fläche mit der Stammfunktion

D(x) = 1/3x^3 - 1/2x^2 - 2x

D(2) - D(-1) = (-10/3) - (7/6) =  -9/2

Die Fläche beträgt also 4,5 Flächeneinheiten.