Schreibweise für die bedingte Wahrscheinlichkeit

Question

Bedingte Wahrscheinlichkeit

40% der Mitarbeiter einer Firma sind Raucher, 30 % der Raucher treibe Sport. Unter den Nichtrauchern beträgt der Anteil der Sportler 45%. Wie groß ist die Wahrscheinlichkeit dafür, dass ein beliebiger Mitarbeiter

a) besonders gesund lebt, d.h. Sport treibt und Nichtraucher ist,

0,6*0,45 =27%

b) sich besonders unvernünftig verhält, d.h. keinen Sport treibt und Raucher ist.

0,4*0,7=28%

Nun muss ich das mathematisch korrekt schreiben...

Das mit P_B(A) ......also ich komme mit der Schreibweise für die bedingten Wahrscheinlichkeit nicht ganz klar.

Was ist P_B(A) 40%? oder 60%? Was ist dann .....

Answer 1

Zu b.)

Sei R das Ereignis Raucher und NS das Ereignis Nichtsportler.

Die Lösung ist nun:

P(R ∩NS)= P(R)*P_R(NS)=0,28

Answer 2

> Das mit P_B(A) ......also ich komme mit der Schreibweise für die bedingte                           > Wahrscheinlichkeit nicht ganz klar.

> Was ist P_B(A) ?

P_A(B) wird oft auch mit P(B|A) bezeichnet und bedeutet

"P(B) unter der Bedingung A"

= Wahrscheinlichkeit von B, wenn man schon weiß, dass das Ereignis A eingetreten ist.

Für die Berechnung gilt die Formel:   P_A(B) = \(\frac{P(A∩B)}{P(A)}\) 

zu a):

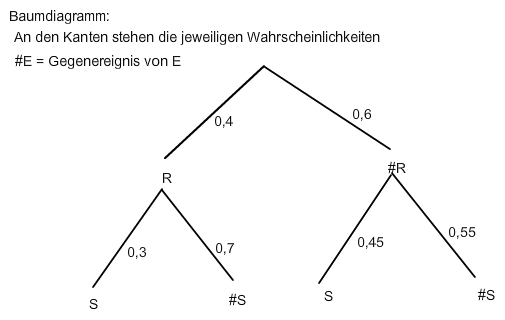
Gesucht ist die Wahrscheinlichkeit dafür, das die Ereignisse   #R und S  beide gleichzeitig eintreten. Diese berechnet sich im Baumdiagramm als Produkt der Wahrscheinlichkeiten des Pfades #R → S

P(S ∩ #R) = P(#R) • P_#R(S) = 0,6 • 0,45 = 0,27 = 27 %

b) analog

Gruß Wolfgang

Comments

"= Wahrscheinlichkeit von B, wenn man schon weiß, dass das Ereignis B eingetreten ist."

Du meinst wohl: "....wenn man schon weiß dass A eingetreten ist"?

---

Danke für den Hinweis Koffi, habe den Flüchtigkeitsfehler  korrigiert.