Hallo Maxi,
ft(x) = x2 - t·x3
ft'(x) = 2x - 3t·x2 = 0 → x = 0 oder x = 2/(3t)
ft"(x) = 2 - 6t ·x
ft"(0) = 2 > 0 → T(0|0)
ft"( 2/(3t) ) = -2 <0 → H( 2 /( 3t) | 4 / (27 t2) )
Der Abstand von H und dem Ursprung beträgt
√((2/(3t))2+(4/(27t2))2) = 2·√(81·t2 + 4) / (27·t2)
Dieser soll 1 betragen:
2·√(81·t2 + 4) / (27·t2) = 1
- mit 27/2·t2 multiplizieren (dann steht die Wurzel allein),
- Quadrieren,
- alles auf eine Seite (...= 0) bringen,
- durch den Faktor bei t4 dividieren.
Dann hast du eine biquadratische Gleichung, die du durch die Substitution z = t2 als quadratische Gleichung mit der pq-Formel lösen kannst.
Lösüngen:
t1,2 = ± √(2·√13/27 + 2/9) ≈ ± 0,7
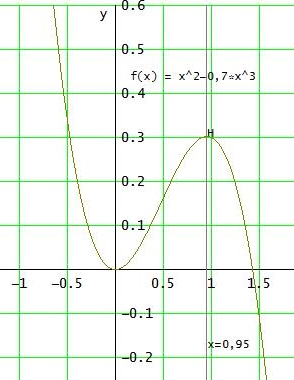
f(x) = x2 - 0,7·x3 oder f(x) = x2 + 0,7·x3
Gruß Wolfgang