Hallo Astrid, wappne dich mit Geduld :-):
gehen wir mal von den beiden Schnittstellen x1 = a und x2 = -2a aus, die nn berechnet hat.
[ wenn du den Satz von Vieta nicht kennst, kannst du die Lösungen von x2 +ax -2a2 = 0 auch mit der pq-Formel ausrechnen:
x2 + px + q = 0
pq-Formel: p = a ; q = -2a2
x1,2 = - p/2 ± \(\sqrt{(p/2)^2 - q}\)
x1,2 = - a/2 ± \(\sqrt{a^2/4 + 2a^2}\) = - a/2 ± \(\sqrt{9/4·a^2}\) = - a/2 ± 3a/2
→ x1 = a ; x2 = -2a ]
Der eingeschlossene Flächeninhalt A ist dann
A = | -2a∫a (g(x) - f(x) ) dx | = | -2a∫a ( -ax + 2a2 - x2 ) dx |
= | [ -1/2·a·x2 + 2a2·x - 1/3·x3 ]-2aa [ Stammfunktionsterm von -ax + 2a2 - x2 ]
Jetzt musst du für x zuerst a und dann -2a einsetzen und die Terme dann subtrahieren:
= | -1/2·a·a2 + 2a2·a - 1/3·a3 - ( -1/2·a·(-2a)2 + 2a2·(-2a) - 1/3·(-2a)3 ) |
= | -1/2·a3 + 2a3 - 1/3·a3 - ( - 2a3 - 4a3 + 8/3·a3) | = | 7/6·a3 - (-10 /3·a3 | = | 9/2·a3 |
Es soll A = 4,5 sein:
| 9/2·a3 | = 4,5 → a3 = ± 4,5 · 2/9 = ± 1 → a = ± 1
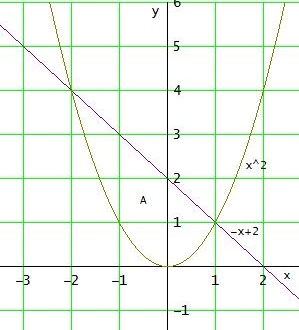
Mit a=1 ist f(x) = -x + 2 und g(x) = x2
Gruß Wolfgang