Hallo ziom,
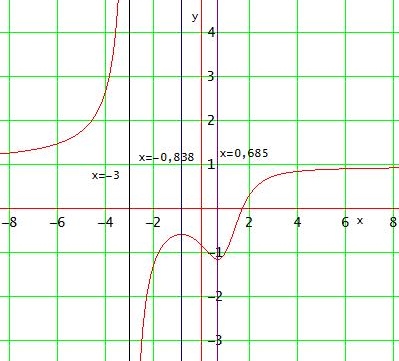
f(x) = (x3 - 5) / (x3 + x2 - 4x + 6) , Monotonieintervalle ↑
Die x-Achse wird durch die Definitionslücken und die Nullstellen von f ' in Intervalle unterteilt, in denen die Steigung f ' ein konstantes Vorzeichen hat, das man durch einfaches Einsetzen von Werten aus den einzelnen Intervallen in die Funktionsgleichung herausfinden kann. So findet man alle Monotonieintervalle mit dem zugehörigen Steigungungsverhalten.
Definitionslücken:
x3 + x2 - 4x + 6 = 0
Man findet x = 3 (Teiler von 6) durch Probieren und führt dann die Polynomdivision
(x3 + x2 - 4x + 6) : (x + 3) = x2 - 2·x + 2 durch.
x2 - 2·x + 2 = 0 ergibt dann keine weiteren reellen Nullstellen.
Nullstellen von f ':
f '(x) = (x4 - 8·x3 + 33·x + 10·x - 20) / (x3 + x2 - 4·x + 6)2 = 0
⇔D x4 - 8·x3 + 33·x + 10·x - 20 = 0
Die beiden reellen Lösungen x1 ≈ 0,6853703660 ; x2 ≈ - 0,8380768377
findest du am einfachsten mit einem Näherungsverfahren (z.B. Newtonverfahren)
Gruß Wolfgang