Diese Funktion ist eine nach unten offene Parabel. Dass sie nach unten offen ist, kann man daran erkennen, dass das Vorzeichen vor dem \(x^2\) negativ ist. Ein erster Eindruck gibt eine Skizze
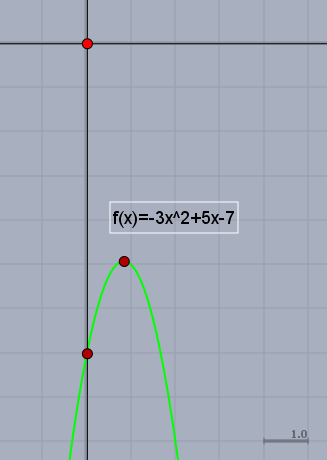
Den Schnittpunkt der Funktion mit der Y-Achse erhält man, indem man \(f(0)\) berechnet. In diesem Fall sehr einfach $$f(0)=-0+0-7=-7 \quad \Rightarrow \quad (0/-7)$$ Den oder die Schnittpunkte mit der X-Achse sind die Nullstellen der Funktion. Die Bedingung ist \(f(x)=0\): $$f(x)=-3x^2+5x-7=0 \quad \Rightarrow \quad x^2-\frac{5}{3}+\frac{7}{3}=0$$ Dies ist eine quadratische Gleichung, welche man mit der pq-Formel lösen kann $$x_{1,2}=\frac{5}{6} \pm \sqrt{\left( \frac{5}{6} \right)^2 -\frac{7}{3}}$$ und diese Gleichung hat keine Lösung im reellen, da der Ausdruck unter der Wurzel kleiner 0 ist. Auch im Graph ist zu sehen, dass die Parabel keinen Schnittpunkt mit der X-Achse hat.
Für den Scheitelpunkt bestimmt man die Ableitung: $$f\prime(x)=-6x+5$$ und setzt diese zu 0 $$f\prime(x)=-6x+5=0 \quad \Rightarrow \quad 6x=5 \Rightarrow x=\frac{5}{6}$$ Einsetzen in die ursprüngliche Funktion ergibt die Koordinaten des Scheitelpunktes $$(\frac{5}{6}/\frac{-59}{12})$$ Gruß Werner
