Wie errechne ich die Koordinaten auf einem bestimmten Vektor wenn der Betrag bekannt ist?

Question

Ich grübel gerade über folgendes Problem:

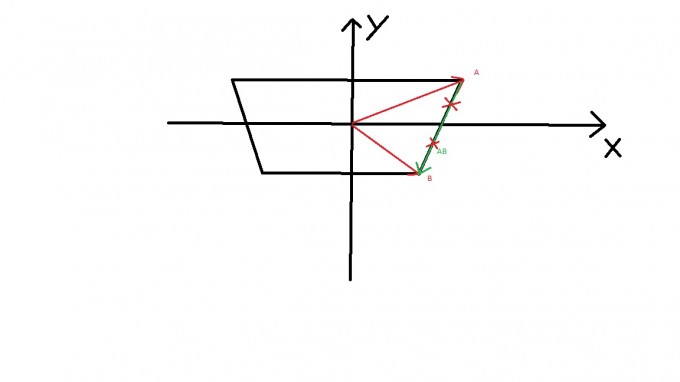
Ich habe ein Trapez in einem zweidimensionalem Koordinatensystem aufgespannt

2 Vektoren sind gegeben, in diesem Fall  $$\xrightarrow { A }$$ = $$\begin{pmatrix} x \\ y \end{pmatrix}$$ und $$\xrightarrow { B }$$ = $$\begin{pmatrix} \frac { x }{ 2 } \\ -y \end{pmatrix}$$.

Aus diesen beiden Vektoren habe ich den Vektor $$\xrightarrow { AB }$$ = $$\begin{pmatrix} \frac { x }{ 2 } \\ 2y \end{pmatrix}$$ berechnet und daraus den Betrag $$\left| \xrightarrow { AB } \right|$$ = $$\sqrt { \frac { { x }^{ 2 } }{ 4 } \times { 4y }^{ 2 } }$$.

Auf dem Vektor $$\xrightarrow { AB }$$ möchte ich nun 2 punkte Berechnen. Einer liegt bei 0,25 der Strecke und der andere bei 0,75. Ich würde also nun den Betrag mit den beiden genannten Zahlen multiplizieren und erhalte 2 Werte.

Wie ermittle ich anhand dieser Informationen meine beiden gesuchten Punkte?

Comments

Hi, es muss $$\overrightarrow{AB} = \begin{pmatrix} -\frac{x}{2}\\ -2y \end{pmatrix}$$sein.

Answer 1

Zunächst mal hast du Vektor BA = A - B ausgerechnet.

Nun nimmst du für deine Punkte

P1 = B + 0.25 * BA = ...

P2 = B + 0.75 * BA = ...

Comments

Also brauche ich den Betrag nicht einmal und musste nur den Vektor um den gesuchten Faktor multiplizieren und anschließend an den Punkt addieren?? :O

Dankeschön :D

---

Genau. Du suchst ja denke ich einen Punkt zwischen A und B der von A genau 1/4 der Strecke von AB entfernt ist oder sehe ich das falsch?