Sollst Du die Fläche des Vierecks ABCE oder die des Fünfecks ABCED berechnen? Ersteres ist in der Zeichnung nicht direkt eingezeichnet (Strecke AE fehlt). Unabhängig davon kann man die Aufgabe wie folgt lösen:
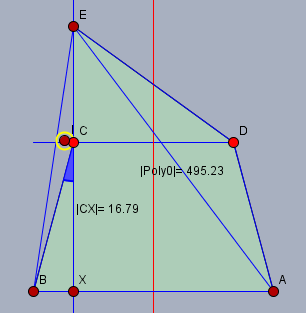
Berechne zunächst die Strecke BX. Da das Trapez gleichschenklig ist, gilt
$$BX=\frac{c}{2}-\frac{a}{2}=\frac{1,5a}{2}-\frac{a}{2}=\frac{1}{4}a=4,5\text{cm}$$
aus dem Dreieck BXC und dem blauen Winkel folgt die Höhe CX des Trapez. Es gilt
$$\tan{(\alpha-90°)}=\frac{BX}{CX} \quad \Rightarrow CX=\frac{BX}{\tan{(\alpha-90°)}}=\frac{a}{4\tan{(\alpha-90°)}}\approx 16,79\text{cm}$$Genauso lässt sich die Seite \(b\) bestimmen
$$\sin{(\alpha - 90°)}=\frac{BX}{b} \quad \Rightarrow b=\frac{BX}{\sin{(\alpha - 90°)}}=\frac{a}{4\sin{(\alpha - 90°)}} \approx 17,39\text{cm}$$ Die Fläche des Vierecks ABCE ist die Summe aus den Flächen der rechtwinkligen Dreiecke BXC und XAE.
$$F_{ABCE}=F_{BXC}+F_{XAE}=\frac{1}{2}BX \cdot CX + \frac{1}{2}XA\cdot (b\cdot 0,75+CX)\\=(37,79+335,64)\text{cm}^2\approx 373,42 \text{cm}^2$$
Die Fläche des Inkreises von BCE erhält man über einen Zusammenhang des Inkreisradius \(r_i\) und der Dreiecksfläche \(F_D\). Es gilt in jeden Dreieck mit den Seiten \(a\), \(b\) und \(c\): \(F_D=r_i \cdot \frac{a+b+c}{2}\). Die Fläche von BCE ist
$$F_{BCE}=\frac{1}{2}BX \cdot b' \approx 29,34\text{cm}^2$$ Von den Seiten des Dreiecks BCE fehlt nur noch BE, welche sich aber leicht über den Pythagoras berechnen lässt. Demnach ist
$$r_i=\frac{2F_D}{b + b\prime + \sqrt{BX^2 + (CX+b\prime)^2}}\approx 0,97\text{cm}$$und seine Fläche \(F_i=\pi{r_i}^2 \approx 2,95\text{cm}^2\).
Gruß Werner