Form einer Rampe Polynomfunktion 3 Grades

Question

Die Rampe muss einen Höhenunterschied von 80cm zwischen 2 Gehwegen ausgleichen. Wie viel Platz in waagrechter Richtung benötigt man wenn der Steigungswinkel maximal 10% betragen darf.

Leider habe ich hierzu keine Idee außer die Ableitungen:

f(x): ax^3+bx^2+c+d

f´(x): 3ax^2+2bx+3c

f´´(x): 6ax+2b

Danke für die Hilfestellung im voraus. Maxi

Ach ja die Lösung sollte lauten 6,805m

Comments

Wie kann denn ein steigungswinkel 10% betragen?

---

Entweder ist die Steigung gemeint: tan (vieh) = 0,1

oder vielleicht sind auch Grad statt Prozent gemeint.

Wie üblich ist der originale Aufgabentext leicht verändert wiedergegeben - aber das ist ja egal, Hauptsache die Aufgabe wird ungefähr richtig gelöst ...

... wer wird denn hier übergenau sein wollen?

Answer 1

an den Anschlusstellen darf der Weg keinen Knick haben. Deshalb muss die Rampe von einem Tiefpunkt T zu einem Hochpunkt H der gesuchten Funktion f verlaufen (oder umgekehrt).

Da jede Polynomfunktion 3. Grades zu ihrem Wendepunkt W symmetrisch ist, kann man das Koordinatensystem so legen, dass W im Ursprung liegt. Dann ist f zum Ursprung symmetrisch und kann mit

f(x) = ax³ + bx   angesetzt werden.        ( f '(x) = 3ax² + b )

der "Platz in waagrechter Richtung" sei p  

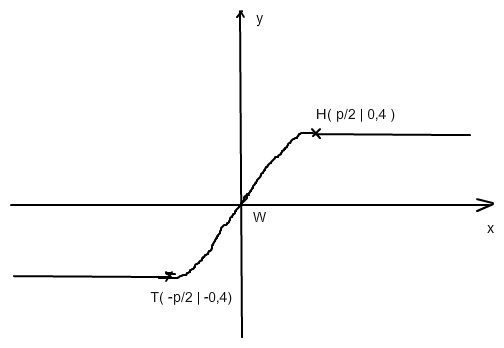
Du kannst jetzt nur die Bedingungen für H oder für T benutzen, weil die jeweils anderen sich aus der Symmetrie ergeben.

f(p/2) = 0,4

f '(p/2) = 0

Damit hast du erst einmal 2 Bedingungen für die 3 Unbekannten a,b und p

Die 3. Bedingung erhält man aus der Angabe für die maximale Steigung m, die -  zwischenT und H - immer im Wendepunkt vorliegt:

  f '(0) = m

Für den Wert von m ist dein  Aufgabentext  allerdings leider unklar:

[[ Steigung 10 % bedeutet  m = 0,1 ]]

Steigungswinkel 10° bedeutet   m = tan(10°)  ≈  0.17633

Mit Letzterem erhält man das angegebene Ergebnis 

Kontrolllösung:

a ≈ - 0,00507638868  ;   b ≈  0,17633  ;  p ≈ 6,805421652   

Gruß Wolfgang

Comments

Die werte lassen sich aber nicht wirklich gut ausrechnen, oder?

---

Es ist lästig, aber es geht - vielleicht auch einfacher -  händig :-) :

a·p^3/8 + b·p/2 = 0.4 

3·a·p^2/4 + b = 0 

 3·a·0² + b = 0.17633   →  b =  0.17633  

mit z = p/2      ;    p = 2z

G1:   a·z³ + b·z = 0.4

G2:  3a·z² + b = 0    →  z = √( -b / (3a))

z in G1:

 a·[√(- b/(3·a))]³ + b·√(- b/(3·a)) = 0.4  | * √(- b/(3·a))

(a·[√(- b/(3·a))]³ + b·√(- b/(3·a)))·√(- b/(3·a)) = 0.4 * √(- b/(3·a))     

a·(- b/(3·a))² + b·(- b/(3·a)) = 0.4 · (- b/(3·a))    | ²

4·b⁴ / (81·a²) = - 4·b / (75·a)

a = - 75/81·b³          →   a = - 0.005076388680 

p = 2 * √( -b / (3a))   →  p =  6.805421652

---

Danke für eure Anworten vorerst einmal!

Sorry für den Tipp Fehler

Ihr habt natürlich recht es handelt sich um 10 Grad und nicht Prozent.

ALso müsste die Bedingung

1. f(0.5)--> 0,4=1/8a+1/4b+1/2c +d

2.f´(0.5)--> 0=3/4a+1b+1/2

3. f´(0)--> 0,17632=c

Stimmt das so jetzt

Dankeschön

---

Das stimmt so nicht, weil du den gesuchten Abstand  p nicht benutzt.

Du musst schon den Ansatz f(x) = ax³ + bx  und die 3 Bedingungen aus meiner Antwort nehmen.

Diese ergeben das Gleichungssystem in meinem Kommentar.

(Vielleicht geht dessen Auflösung auch einfacher :-))

---

Aber deine Lösung ist mir zu Hoch. Skizze ist klar der Rest leider nicht bis auf die Ableitung vielleicht noch. Danke aber für die Mühe.

Bin Dankbar wenn jemand eine einfachere Lösung anbieten könnte.

Answer 2

Mach eine Skizze und lege ein Koordinatensystem über das Fiasko.

Nehmen wir mal an, an der Stelle Null sei die Höhe 0,8 und an der Stelle a sei die Höhe Null.

An den Stellen Null und a ist die Steigung minus 0,1.

Deine Ableitung hat übrigens einen dezenten Tippfehler.

Comments

> An den Stellen Null und a ist die Steigung minus 0,1.

Bist du sicher, dass du mit der "Stelle a" den Koeffizienten von x³ meinst?

---

Nein, den Koeffizienten von x^3 habe ich nicht gemeint.

Nennen wir die Stelle, die gesucht werden soll, S, um keine weiteren Verwechslungen zu vermeiden.

---

S ist auch blöd - nachher meint noch jemand, das wäre der Scheitelpunkt.

Vielleicht dann doch "w" wie "woisserdenn?"

---

EDIT:

An den Stellen Null und a ist die Steigung 0.

(sorry für meine Unaufmerksamkeit)

---

Ich dachte, wir hätten uns auf "w" geeinigt  :-)