Steigung einer gespiegelten Geraden

Question

ich suche die Formal zur Berechnung der Steigung einer gespiegelten Geraden.

Bekannt sind

a) die Steigung der Spiegelachse

b) die Steigung zu spiegelnden Geraden

Gibt es für diesen Zweck eine Formal ?

Hintergrund : In einer animierten Grafik soll ein Ball (dessen Bewegung eine Gerade ist ) bei Aufprall an einer beliebigen Achse in der neu zu berechnenden Richtung "abprallen".

Danke und Gruß

Axel

Answer 1

Also spiegelst du an dem Lot zur auftreffenden Geraden.

Den Auftreffpunkt hast du ja wahrscheinlich und kannst den

als Nullpunkt nehmen.

Dann einfach zu einem Punkt auf der Geraden vorher das

Spiegelbild berechnen. Das geht , wenn die auftreffende

Gerade den Winkel α mit der x-Achse bildet so. Die folgende Matrix

mit den Koordinaten des

Originalpunktes in dem so beschriebenen Koordinatensystem

multiplizieren


cos(2α)     sin(2α)
sin(2α)    - cos(2α)

Answer 2

Es gilt Einfallswinkel = Ausfallswinkel

gegeben
tana, tanb : Steigungen
arctan(tana) = alpha
acrtan(tanb) = beta

Steigung Ausfallswinkel Ball tan(gamma)

Soweit meine Überlegungen

mfg Georg

Comments

Hallo Axel,
gib einmal 2 Steigungen als Beispiel an.
Fürs erste und einfachste zwei 2 positive
Steigung  z.B.
Ball : 15 °
reflektierende Fläche : 60 °

---

Hallo Georg,

in meinem Code drückt sich die Steigung in einem Steigungsdreieck aus:

z.B. hat ein Ball die Eigenschaften speedX und speedY, was bei den Werten 3 und 1 eine Steigung von 1/3 ergibt. Sicherlich gibt es eine Formel, mit der ich den Winkel zur X-Achse berechnen kann.

Analog müsste auch ein Winkel der zweiten Gerade  zu berechnen sein.

All das erscheint mir im Moment unnötig kompliziert.

 Wenn ich Dich richtig verstanden habe, würde man daraus direkt die gewünschte Steigung berechnen können.

Ich probier das gleich mal aus und melde mich. Muss nur noch nach dem Begriff "arctan" googeln.

VG

Axel

---

Hallo Axel,

du hast nur relativ wenig mathematische Kenntnisse .

ich war / bin selbst Programmierer und meine
so etwas ähnliches schon einmal programmiert
zu haben.

ich schaue bei mir einmal nach. Was für eine
Programmiersprache nutzt du ?

Mach dir jetzt erst einmal keine Arbeit.

---

Hi Georg,

Danke,ich möchte mir aber gerne Arbeit machen ;-)

Da die Grafik im Browser angezeigt werden soll, verwende ich JavaScript.

Und: Ja, mit Trigonometrie hab ich eher wenig Erfahrung.

Frage :

tana, tanb : Steigungen 
arctan(tana) = alpha 
acrtan(tanb) = beta 

Die Funktion arctan(m) gibt mir den Winkel im Bogenmaß. Heisst : Jetzt noch jeweils das Bogenmaß in Grad umrechnen, dann 180 - Summe der 2 Winkel , zurück ins Bogenmaß und mit tan(rad) neue Steigung ermitteln. (eventuell auch ohne Umweg rad -> Grad)

Richtig ?

Danke und Gruß

Axel

---

Ich habe folgende Lösung ersonnen

m1:= -0.7; | Steigung einfallswinkel
m2:= 0.2;   | Steigung reflektiernde Fläche
m3:= m1*(-1); | Steigung reflektierter Strahl
w2:=arctan(m2); | Winkel reflektierende Fläche
w3:=arctan(m3); | Winkel reflektierter Strahl
w4:= w3 + w2; | Ausfallwinkel
m4:=tan(w4); | tan / Steigung des Ausfallwinkel

Blau : einfallender Strahl auf rote Fläche
( von links oben )

Grün : reflektierter Strahl nach rechts oben

Erklärungen kommen noch.

---

m1:= -0.7; | Steigung einfallswinkel
m2:= 0.2;   | Steigung reflektiernde Fläche
m3:= m1*(-1) = 0.7
w2:=arctan(m2) = 0.197 in Bogenmass 11.29 °
w3:=arctan(m3) = 0.61
w4:= w3 + w2 = 0.808
m4:=tan(w4); | 1.046

Erklärung kommt heute nachmittag

---

Stimmt alles noch nicht.
Bitte warte ab bis ich die richtige
Lösung gefunden habe.

---

w1:=arctan(m1);
w2:=arctan(m2);
w3:=w1-w2;
m3:=tan(w3);
m3:=-m3;
w3:= arctan(m3);
w3 := w3 + w2;
m3:= tan(w3);

m1 ( Ball ) und m2 ( auf Fläche ) sind die
Steigungen.
m3 die Steigung des reflektierten Balls

Bedingungen
m1 ungleich m2

Die Winkel von m1 und m2 ungleich 0,90,180,
270,360 °

Wenn es dir möglich ist :
Bau diesen Quelltext in dein Programm
ein und überprüfe die Richtigkeit
direkt in einer bewegten Grafik.
Dies wäre die einfachste Testmethode

---

Hallo Georg,

zunächst danke für deine Überlegungen.

Ich kann Deinen Schritten noch nicht ganz folgen

Warum weist Du m3 3 mal unterschiedliche Werte zu ?

_{m3:=tan(w3); 
m3:=-m3; 
...}

_{m3:= tan(w3);}

Leider bist Du nicht auf meine vorherigen Ideen eingegangen. Es hätte mich interessiert, was Du dazu sagst.

Anhand folgender Beispielskizze habe ich nun einen konkreten Plan entwickelt : (blau ist die Mauer, orange die Flugbahn der Kugel )

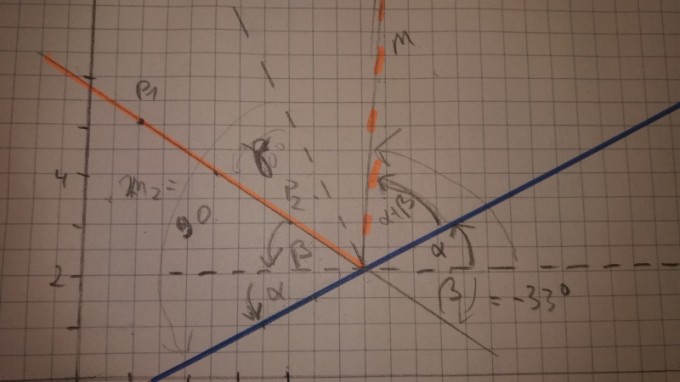
Wie man sieht, sind α und β bekannt. Daraus ergibt sich :

Winkel nach Aufprall = 2 * α + β

Da mein β leider einen negativen Winkel ergab, habe ich daraus die Formal

"Winkel nach Aufprall = 2 * α - β" gemacht. Eine Begründung kann ich hier nicht liefern ;-(

Dadurch entstand folgender Code, der alle bisherigen Tests bestand (reine Berechnungen):

function m(){

  var m1 = document.getElementById("m1");

  var val1 = eval(m1.value);

  var at1 = Math.atan(val1);

  var wk1 = at1*180/Math.PI;

  var m2 = document.getElementById("m2");

  var val2 = eval(m2.value);

  var at2 = Math.atan(val2);

  var wk2 = at2*180/Math.PI;

  var wk3 = 2*wk1-wk2;

  var at3 = wk3/180*Math.PI;

  var m3 = Math.tan(at3);

  document.getElementById("m3").value = m3;

  document.getElementById("at1").value = at1;

  document.getElementById("at2").value = at2;

  document.getElementById("at3").value = at3;

  document.getElementById("wk1").value = wk1;

  document.getElementById("wk2").value = wk2;

  document.getElementById("wk3").value = wk3;

}

Dieser muss nun freilich noch in das Programm, das die Grafik erzeugt, eingebunden werden.

Ich melde mich, wenn das passiert ist, für weitere Erläuterungen bin ich jetzt zu müde ,,,

VG

Axel

---

Leider bist Du nicht auf meine vorherigen Ideen
eingegangen. Es hätte mich interessiert, was
Du dazu sagst.

Sag ich noch.

ich wollte mich zunächst darauf konzentrieren eine
eigene Lösung zu entwickeln.

Deine Ausarbeitungen schaue ich mir auch an.

Warum weist Du m3 3 mal unterschiedliche Werte zu ?

m3:=tan(w3); 
m3:=-m3; 
...
m3:= tan(w3);

m3 ist zunächst eine Zwischenvariable der
verschiedene Werte zugewiesen werden.
Sie ist aber immer der Tangens des Ausfall-
winkels.

ich würde gern eine konkrete Berechnung
anhand deines Beispiels durchführen.

Dabei sollten wir uns an die üblichen
Winkel Definitionen halten


Ein Winkel wird angegeben im Urspung beginnend
gegen den Urzeigersinn gedreht . Eigentlich genau wie
dasKoordinatensystem auch:
0 ° waagerecht nach rechts.
90 ° senkrecht nach oben
180 ° waagerecht nach links
270 ° senkrecht nach unten
360 ° wieder waagerecht nach rechts

315 ° kann auch als -45 ° geschrieben werden.
Alle trigonometrischen Funktion können damit
arbeiten.

Als Eingangsvariable sind anzugeben.
m1 : tan des Ballwinkels
m2 : tan des Mauerwinkels

Bitte gib diese 2 Werte an.

Du kannst auch die Winkel in Grad oder Bogenmass
angeben.

Orange ca 135 °
Blau ca 40 °

mfg Georg

Du kannst auch die in meinem Profil angegebene Internetadresse
nutzen.

---

Hi Georg,

Es ist Wochenende und ich hatte nicht so viel Zeit zum Weitermachen.

In meiner Berechnung steckt noch ein Fehler, den ich jetzt gefunden habe, und zwar in der Berechnung des Winkels. Hier der Code (erst aus der Steigung den ArcTan ermitteln und daraus den Winkel in Grad :

  var m1 = document.getElementById("m1");

  var val1 = eval(m1.value);

  var at1 = Math.atan(val1);

  var wk1 = at1*180/Math.PI;

und hier das Resultat :

Bei Steigung = -5 hätte ich einen Winkel von 102 erwartet anstatt 78. 102 Grad von der X-Achse aus gemessen. Das würde bedeuten, dass der Winkel aus dem ArcTan anders ermittelt werden muss. 

Sehe ich das so richtig ?

VG

Axel

---

-5 bedeutet 
x um 1 Einheit nach rechts
y um 5 Einheiten nach unten

Dies bedeutet
a = 281.31 °
( 270 ° ist die y-Achse senkrecht nach unten
oder a = -78.69 ° ( mein Taschenrechner )
( 78.69 mit dem Uhrzeigersinn )

Gib einmal wie vorgeschlagen die beiden
Steigungen an.

Orange ca 135 ° : m1 = -1
Blau ca 40 ° : m2 = 0.839

mfg Georg

---

Hi

Folglich ist meine Berechnung, aus der ich den Ausfallswinkel berechne, nicht korrekt:;

var wk3 = 180 - (2*(wk1-wk2)+wk2);

VG

Axel

---

bevor wir den 7.Schritt tun sollten wir den
ersten tun.

es werden 2 Winkel übergeben
blau : die spiegelnde Fläche
rot : der Ball

Winkel in Grad ( 0 <= x <= 360 ) oder
Bogenmaß 0 <= x <= 2 * pi

Sie Skizze zeigt dir die Winkel.

mfg

Answer 3

Lege den Punkt. in dem der Ball auf die Gerade mit der Steigung m trifft, in den Koordinatenursprung. Sei m₁ die Steigng der Flugbahn des Balles. Dann ist der Winkel β zwischen m₁ und m₂=1/m zu berechnen mit der Formel tan(β)=I(m₁-m₂)/(1+m₁m₂)I. Wähle einen beliebigen Punkt P(x/m₁x) auf der Flugbahn des Balles und drehe ihn im Winkel α=2β um (0/0) mit Hilfe der Drehmatrix

cos(α)   -sin(α)

sin(α)    cos(α)

Der gedrehte Punkt sei Q(a/b). Dann ist die Flugbahn des Balles nach Abprall von der Geraden y=bx/a.

Comments

vielen Dank für die vielen Antworten, die alle unterschiedliche Lösungsansätze bieten und von denen ich auf Anhieb keine wirklich verstanden habe.

Die Ausgangssituation ist momentan folgende:

- es wird eine Berührung der beiden Objekte erfasst

- die beiden Steigungen sind bekannt

Meine Vermutung war, dass ich anhand der beiden Steigungswerte die neue Steigung berechnen kann. Nach dem Lesen Eurer Antworten bin ich mir da nicht mehr so sicher.

Leider ist der Koordinatenpunkt der Berührung noch nicht bekannt, so dass ich diesen aktuell nicht bei der Berechnung heranziehen kann.

... Eventuell wäre die Frage in einem Entwickler-Forum besser aufgehoben ...

Ich danke Euch und freue mich weiterhin auf neue Ideen.

Gruß

Axel

---

Hallo Axel, du schreibst "Leider ist der Koordinatenpunkt der Berührung noch nicht bekannt, so dass ich diesen aktuell nicht bei der Berechnung heranziehen kann".

Mein Vorsahlag, den Koordinatenpunkt der Berührung als (0/0) zu wählen, ist legitim, da es nur um Steigungen geht (Steigungen gegeben, Steigung gesucht).

Dann schreibst du "Meine Vermutung war, dass ich anhand der beiden Steigungswerte die neue Steigung berechnen kann. Nach dem Lesen Eurer Antworten bin ich mir da nicht mehr so sicher."

Was verunsichert dich da? Meine Lösung endet doch mit der gesuchten Steigung b/a.

---

Hallo Roland,

Du schreibst :"Wähle einen beliebigen Punkt P(x/m₁x) auf der Flugbahn des Balles und drehe ihn im Winkel α=2β um (0/0) mit Hilfe der Drehmatrix ".

Hier ist schon das 1. Problem: Ich habe weder Papier noch Geodreieck zur Verfügung.

Weiterhin ist mir der Begriff der "Drehmatrix" noch gänzlich unbekannt.

VG

Axel

---

Papier und Geodreieck sind ganz überflüssig, wenn man den Begriff der Drehmatrix kennt. Will man die Aufgabe ohne diesen Begriff lösen, lässt, muss man  Georgs Lösung verwenden.

---

OK, danke.

Jetzt muss ich nur beim kleinen 1X1 wieder anfangen (hier Sinus und Cosinus), um zu verstehen, wie ich die Regel der Drehmatrix  anwenden kann.

Bei Fragen melde ich mich (also höchstwahrscheinlich)

VG

Axel

---

Du kannst stattdessen auch den von Georg(born) vorgeschlagenen Lösungsweg wählen. Nachfragen sind jederzeit willkommen.