Du fragst. "wie hast du erkannt, dass es sich um Ähnliche Dreiecke handelt?" Nun - ich sehe das - aber die Frage ist doch: "wie siehst Du das?"
Zeichne dazu die Winkel in den Dreiecken ein:
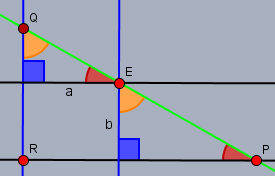
Die beiden schwarzen horizontalen Geraden sind per Definition parallel, weil ich die obere der beiden parallel zur unteren (der X-Achse) eingezeichnet habe. Die Winkel bei den Punkten \(P\) und \(E\) (die roten) sind sogenannte Stufenwinkel. Und Stufenwinkel an Parallelen sind gleich. Das gleiche gilt für die orangen Winkel mit den blauen senkrecht verlaufenden Parallelen. Und die rechten Winkel (in blau) sind auch gleich. D.h. wir haben hier zwei Dreiecke, deren drei Winkel alle gleich sind - folglich sind sie ähnlich.
Du fragtest: "wie kann ich aus der Aufgabe herauslesen, dass ich keinen Abstand brauche"
weil nirgends weder ein 'Abstand' selbst noch ein Hinweis darauf erwähnt wurde.
Du schreibst: "Es geht also darum, um Verhältnisse in einem Dreieck zu erkennen, wie du eben mit y-b/a = b/P'P ausgedrückt hast. Dort habe ich Schwierigkeiten. "
Du könntest statt dessen auch den (2.)Strahlensatz bemühen. Betrachte dazu die blauen Parallelen, die von den Geraden durch \(PQ\) (grün) und \(PR\) (schwarz) geschnitten werden. Es ist
$$\frac{y}{b}=\frac{x}{x-a} \quad \Rightarrow y=\frac{bx}{x-a}$$
.. ich habe die erste Gleichung dazu mit \(b\) multipliziert.
Du kamst bis: "ADreieck(x) = (2400x)/(x-60) + 40x I Für addition Bruch erweitern mit (x-60)
ADreieck(x) = (2400x)/(x-60) + 40x(x-60) "
beim zweiten Term fehlt noch "/(x-60)" also
$$A_{\text{Dreieck}}= \frac{2400x}{x-60} + \frac{40x(x-60)}{x-60}= \frac{2400x}{x-60} + \frac{40x(x-60)}{x-60}\\=\frac{2400x}{x-60} + \frac{40x^2-2400x}{x-60}=\frac{2400x +40x^2-2400x}{x-60}\\=\frac{40x^2}{x-60}$$
Du fragtest auch noch: " Und welche Mathematischen Kenntnisse fehlen mir, damit ich die Verhältnisse in einem Dreieck und deren Ähnlichkeit kenne?" Übung - Mathematik lernt man nicht durch Zuhören oder Zusehen. Mathematik musst Du tun, um es zu lernen.
Gruß Werner