Berechnen Sie das folgende unbestimmte Integral: ∫ xe^{-x²} dx

Question

Berechnen Sie das folgende unbestimmte Integrale

\( \int x e^{-x^{2}} \mathrm{~d} x \)

Ist es einfach nur die Fläche berechnen oder was ist mit unbestimmtes Integral gemeint?

Answer 1

Huhu,

Nutze die Subst.

-x^2 = z

-2x dx = dz

-1/2*∫e^z dz

= -1/2*e^z + c    |Resubst

= -1/2*e^{-x^2} + c

Grüße

Comments

.. also muss ich einfach nur das integral finden...

---

Wie meinst Du das? Das Integral von e^z sollte ja kein Problem sein. Der einzige Trick war die Substitution. Wenn man das ein paar Mal gemacht hat, geht das recht schnell ;).

Answer 2

hierbei geht  es um Integration mittels Subsitution:

z= -x^2

dz/dx= -2x

dx= dz/(-2x)

Das setzt Du in den Integranden ein.

= -1/2∫ e^z  dz

= -1/2 e^z +C

= -1/2 e^{-x^2} +C

Answer 3

Beim unbestimmten Integral sind keine Grenzen
/ Abschnitte angegeben. Es handelt sich um die
Aufstellung der Stammfunktion.

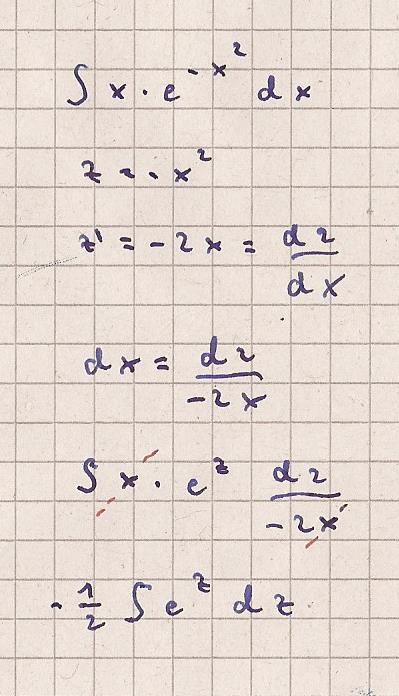
-1 / 2 *  e^z + C
-1/ 2 * e^{-x^2} + C

Noch ein passender Witz

2 Mathematiker sind in einem Cafe und bestellen etwas. Der eine
Mathematiker geht nach einer Weile zur Toilette. Zwischenzeitlich
bringt die Kellnerin einen Teil der Bestellung und der verbliebene Mathematiker sagt " Sie können mir einen Gefallen tun. Antworten
Sie beim nächsten Mal auf meine Frage mit
" x hoch 3 geteilt durch 3 ".

Die Kellnerin verspricht dies zu tun und murmelt beim Weggehen
" x hoch 3 geteilt durch 3 ".

Der 2.Mathematiker kommt zurück und es entwickelt sich ein Gespräch
über die mathematischen Fähigkeiten der Bevölkerung.
Der erste Mathematiker sagt diese seien schon recht gut und will
dies demonstrieren.
Er fragt die nunmehr an den Tisch kommende Kellnerin " Was ist die Stammfunktion von x^2 ". Die Kellnerin " x hoch 3 geteilt durch 3 ".

Der Kollege ist begeistert. Die Kellnerin geht wieder, dreht sich aber noch einmal um und sagt " plus c ".

Comments

Den finde ich echt stark und passend. :-)

Wahr aber wahrscheinlich doch eine Aushilfsstudentin   :-)

---

Falls die Anekdote nicht wahr ist dann ist sie
zumindest gut erfunden.