Hallo Linda.
Natürlich gibt es analog zur pq-Formel auf für Gleichungen 4. Grades eine exakte PQRSTUVW-Formel -> ABER die kommt selbst für Mathematiker erst später im Studium dran und beinhaltet komplexe Zahlen und zig ineinander verschachtelte Wurzeln!
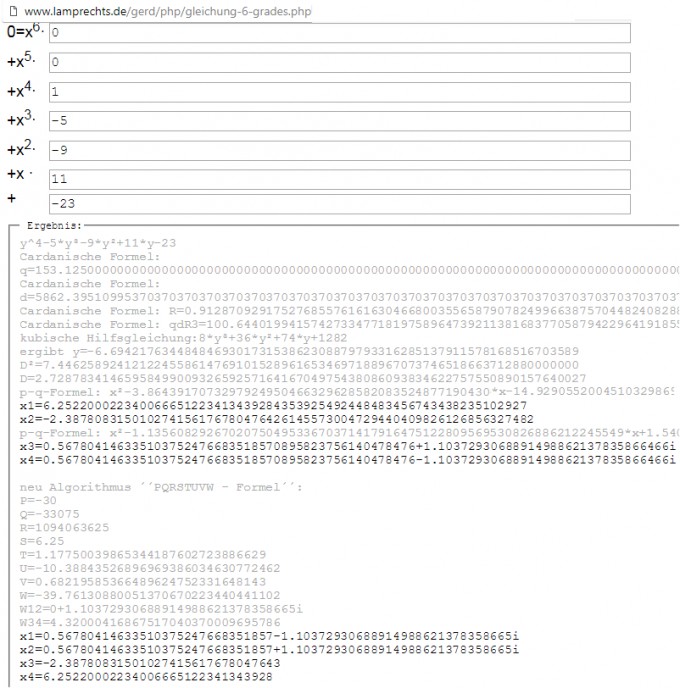
unter http://www.lamprechts.de/gerd/php/gleichung-6-grades.php
werden 2 Algorithmen vorgerechnet, die ABER NIE im Abi drankommen geschweige abgefragt werden -> und schon lange nicht ohne Taschenrechner (über 10 ineinander verschachtelte 2. und 3. Wurzeln ! ).
Das ist es ja gerade, dass sich die Lehrer extra für Euch leichte "Sonderfallaufgaben" ausdenken, wo:
- entweder was herauszukürzen geht
- nur Grad 2 und Grad 4 vorhanden ist und man durch Substitution eine pq-Formel anwenden kann
- eine ganzzahlige Nullstelle zw. -4 und 4 leicht zu erraten ist
Das Newton-Verfahren (näherungsweise Annäherung) geht immer (egal welcher Grad) -> benötigt aber immer einen Taschenrechner -> wenn Ihr ohne diesen lösen sollt, fällt das schon mal raus!
Deine Aufgabe (selbst ausgedacht oder falsch abgeschrieben) gehört nicht zu denen, die im ABI:
- je drankommen werden
- für Euch als Lösung explizit aufzuschreiben gehen (ohne Hilfsvariablen etwa eine ganze DIN-A4 Seite voll)
- mit mehr als 6 Nachkommastellen auszurechnen gehen (selbst Taschenrechner mit "solve" rechnen oft nur 6 Stellen genau!)
- komplexe Zahlen dann auch noch irrational (also unendlich viele Nachkommastellen) kommt nicht dran!
Was höchstens drankommen kann, ist den Verlauf grob abschätzen:
- wieviele reelle Nullstellen
- in welchen Bereich liegen sie
Oder Du sollst keine Nullstellen, sondern die Ableitung berechnen (Optimierungs- oder Extremwertaufgabe -> da wird von der Ableitung die Nullstelle gesucht).