Hallo Bango,
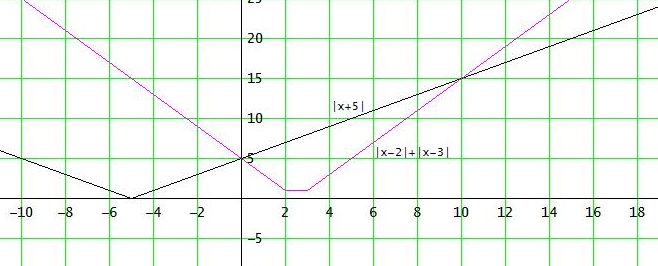
⎮x - 2⎮ + ⎮x - 3⎮ ≥ ⎮x + 5⎮
Betrachte die einzelnen Intervalle zwischen den Nullstellen der Terme in der Beträgen. In diesen Intervallen kannst du die Beträge jeweils auflösen, indem du den Betrag
- weglässt, wenn der Term im Betrag ≥ 0 ist
- den Term im Betrag negativ nimmst, wenn dieser < 0 ist:
1. Fall:
⎮x - 2⎮ + ⎮x - 3⎮ ≥ ⎮x + 5⎮ ∧ x < - 5
⇔ - x + 2 + (-x+3) ≥ - x - 5 ∧ x < - 5
⇔ x < - 5 → L1 = ] - ∞ ; - 5 [
2. Fall:
⎮x - 2⎮ + ⎮x - 3⎮ ≥ ⎮x + 5⎮ ∧ x ≥ - 5 ∧ x < 2
⇔ - x +2 + (-x+3) ≥ x + 5 ∧ x ≥ - 5 ∧ x < 2
⇔ -5 ≤ x ≤ 0 → L2 = [ - 5 ; 0 ]
3. Fall:
⎮x - 2⎮ + ⎮x - 3⎮ ≥ ⎮x + 5⎮ ∧ x ≥ 2 ∧ x ≤ 3
⇔ x - 2 + (- x + 3) ≥ x + 5 ∧ x ≥ 2 ∧ x ≤ 3
keine Lösung → L3 = { }
4. Fall:
⎮x - 2⎮ + ⎮x - 3⎮ ≥ ⎮x + 5⎮ ∧ x > 3
⇔ x - 2 + x - 3 ≥ x + 5 ∧ x > 3
⇔ x ≥ 10 → L4 = [ 10 ; ∞ [
L = L1 ∪ L2 ∪ L3 ∪ L4 = ] - ∞ ; 0 ] ∪ [ 10 ; ∞ [
Gruß Wolfgang