Polardarstellung der Division (Komplexe Zahlen)

Question

Folgendes Problem, ich habe ein Beispiel zur Division der Polardarstellung komplexer Zahlen, mit den komplexen Zahlen z1 und z2:

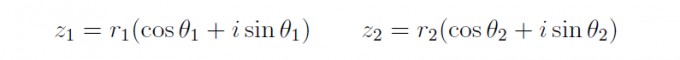
Diese sollen nun miteinander dividiert werden:

 

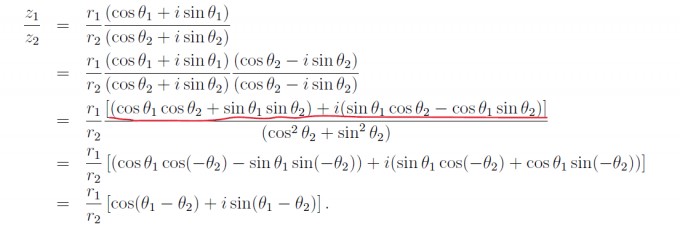
Als Hilfestellung sind noch die Additionstheoreme von Sinus und Cosinus gegeben:

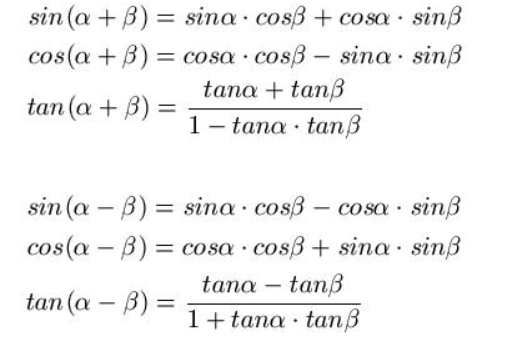
Nun verstehe ich alles bis zu dem Punkt, wo der Nenner verschwindet (also der Teil nach dem roten Strich. Wenn man den rot unterstrichenen Teil mittels des Additions- bzw. Subtraktionstheorem auflöst, dann kommt man ja direkt auf die finale Lösung, bloß verstehe ich nicht was mit dem Nenner passiert. Im vorletzten Schritt werden nur die Vorzeichen verändert, aber grundsätzlich bleibt es ja genau dasselbe und man kommt auf das gleiche Ergebnis, nur ist der Nenner auf einmal weg. Kann mich da jemand aufklären?

Liebe Grüße :)

Comments

Ich gehe davon aus, dass "cos²(φ)+sin²(φ)" = 1 ist, aber warum ist das der Fall?

Answer 1

Es gilt allgemein:

sin^2(x) +cos^2(x)=1 Das ist der trigonometrische Pythagoras .

Wenn Du im Einheitskreis ein rechtwinkliges Dreieck einzeichnest, wird schnell klar, warum der Satz gilt. sin(x) und cos(x) sind die beiden Katheten (der Nenner ist 1, fällt also weg), 1 ist die Hypotenuse.