Der Graph von f(x) = f(x) = 0,4·x4 + 1,8·x2 + 2,3 passt eindeutig zu meinem Bild.
Der in der Lösung angegebene passt zu
f(x) = 0,4·x4 - 1,8·x2 + 2,3 ( vergößert, D = [ -1,5 ; 1,5 ] )
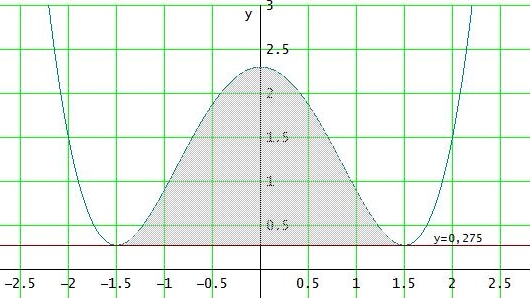
und das sieht natürlich sinnvoller aus
Wenn nicht ein Fehler im Aufgabentext vorliegt, hättest du die Nachfrage von Koffi sorgfältiger prüfen müssen :-)
Die beiden Tiefpunkte sind ( ± 1,5 | 0275 )
In c) ist mit der "Höhe 1,5m" ist jetzt einfach y = 1,5 gemeint
du musst für die Breite die Gleichung 0,4x4 - 1,8x2 + 2,3 = 1,5 lösen:
(analog zu 0,4x4 - 1,8x2 + 2,3 = 3 in der Antwort )
x1,2 ≈ ± 0,707 ; x3,4 = ± 2 ∉ [ - 1,5 ; 1,5 ]
→ Glockenbreite dort oben ist 1,414 m
In b) ist die Höhe der Glocke allerdings 2,3m - 0,275m = 2.025m
(die Glocke reicht bis in f(0) = 2,3m Höhe, ist aber nicht so hoch!)