mach dir zuerst eine Skizze, da hat auch Wiki was parat ;)
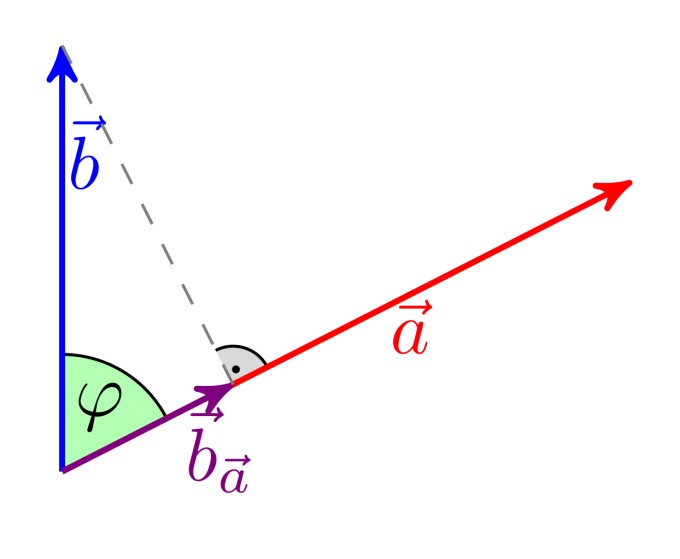
(Hier sind allerdings a und b im Bezug zur Aufgabe vertauscht).
Zuerst Berechnet man die parallele Komponente, diese ergibt sich aus
$$ \vec{a}_{||}=|\vec{a}_{||}|*\frac{\vec{b}}{|\vec{b}|} $$
Jetzt braucht man noch den Betrag von a_|| . Der ergibt sich mithilfe des Winkels zu:
$$ \vec{a}_{||}=|\vec{a}_{||}|*\frac{\vec{b}}{|\vec{b}|}=cos(\varphi)*|\vec{a}|\frac{\vec{b}}{|\vec{b}|} $$
Den cos(φ) bekommst du mithilfe des Skalarprodukts
$$cos(\varphi)*|\vec{a}|\frac{\vec{b}}{|\vec{b}|}\\=\frac{(\vec{a}*\vec{b})}{|\vec{a}||\vec{b}|}*|\vec{a}|\frac{\vec{b}}{|\vec{b}|}\\=(\vec{a}*\vec{b})*\frac{\vec{b}}{|\vec{b}|^2}=(-7)\frac{\begin{pmatrix} 2\\-1\\3 \end{pmatrix}}{14}=\begin{pmatrix} -1\\1/2\\-3/2 \end{pmatrix} $$
Die senkrechte Komponente ergibt sich aus dem Ansatz
$$\vec{a}=\vec{a_{||}}+\vec{a}^{\bot} $$
zur gegebenen Lösung.
(Zu deiner letzten Frage: nein, man kann Vektoren nicht dividieren. Man kann durch den Betrag teilen.)