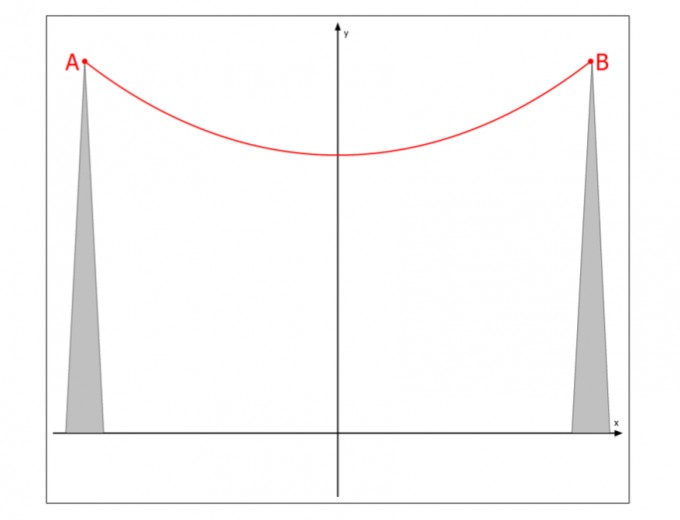
17 Aufgabe: Ein Seil durch die Punkte A := (−20; h) und B = (20; h) werde modelliert durch die Funktion f(x) := 22 cosh(0, 04x).
(a) In welcher Höhe ist das Seil befestigt?
Antwort: 29,42m
(b) Wie tief hängt es durch?
0; 22 also es hängt 7,42m runter
(c) Welchen Winkel α bildet das Seil mit den Stäben?
hier brauchen wir hilfe ???????
(d) Bestimmen Sie die Gleichung der Parabel p (x) = ax2 + bx + c durch die Punkte A und B mit
1
dem gleichen Winkel α aus Teil (c).
(e) Was hängt tiefer und wie groÿ ist die Di erenz?
(f) Bestimmen Sie die Fläche zwischen f und p1, wenn bekannt ist, dass die beiden Funktionen im
Intervall (−20; 20) keine weiteren Schnittpunkte haben.
(g) Bestimmen Sie die Gleichung der Parabel p (x) = ax2 + bx + c durch die Punkte A und B und
2
durch den tiefsten Punkt der Funktion f.
(h) Bestimmen Sie die Fläche zwischen f und p2.
(i) Was ist eine bessere Näherung, p1 oder p2, wenn man die Gröÿe des Flächeninhaltes als Kriterium heranzieht?