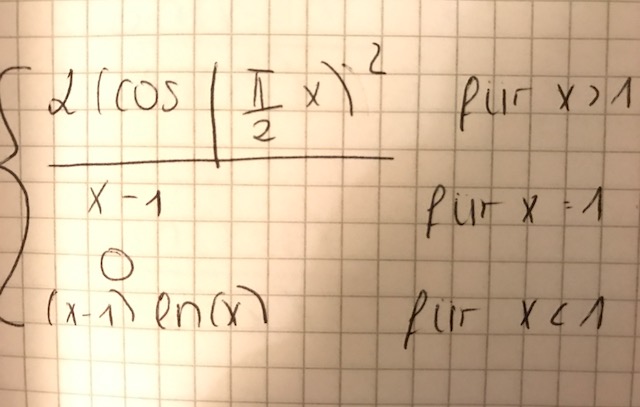Vom Duplikat:
Titel: Hopital Grenzwerte Stetigkeit
Stichworte: hospital,grenzwert
Folgende Aufgabenstellung.
1. Bestimme a ∈ R, für welche die Funktion fa in x0=1 stetig ist
2.Bestimme alle a∈R, für die die Funktion fa in x0=1 stetig ist.
Ich wäre dankbar für eine ausführliche Rechnung/Erklärung. Leider scheint bei mir das Ergebnis nicht mit dem aus der Lösung übereinzustimmen.