Bitte helfen Sie mir mit dieser Aufgabe.
Es seien x, y, z ∈ Rn. Zeigen Sie:
(a) Es gilt ΙΙxΙΙ − ΙΙyΙΙ ≤ ΙΙx − yΙΙ
(b) Es gilt ΙΙxΙΙ= ΙΙyΙΙ genau dann, wenn x − y und x + y aufeinander senkrecht stehen.
(c) Sind x und y ungleich 0, dann gilt
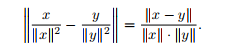
(d) Es gilt ΙΙx − yΙΙ * ΙΙzΙΙ ≤ ΙΙy-zΙΙ*ΙΙxΙΙ + ΙΙz-xΙΙ*ΙΙyΙΙ
.