Homogenität: Wie errechne ich den Grad der Homogenität, wenn ich ausschliesslich Lampda gegeben habe?

Question

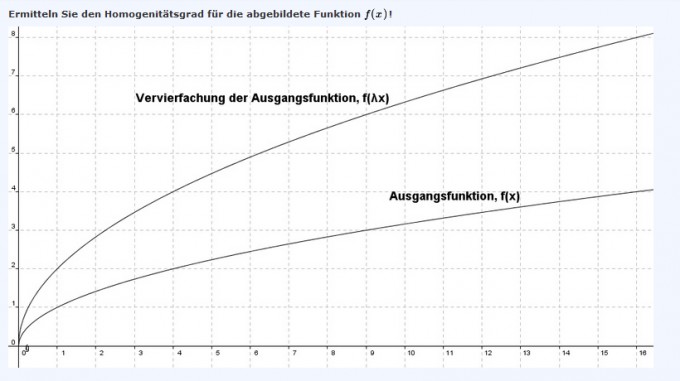
Ich kenne nur die Vorgehensweise wenn man die Funktion gegeben hat.

1.) Ersetze jedes x durch λx

2.) Versuche, λ^r auszuklammern

3.) Ist f(λx) = λ^r * f(x), so ist f homogen von Grad r

4.) Gilt die Gleichung nicht, dann ist f nicht homogen

Aber wie diese Aufgabe (auf den beiden Bildern) gestellt ist, kann ich sie nicht lösen. Vor allem die Lösung verwirrt mich, mit ihr kann ich leider noch weniger anfangen.

Answer 1

Wir haben den Graph der Funktion f(x) und auch von f(4x). 

Für x=1 haben wir $$f(1) = 1 \ \text{ und } \ f(4\cdot 1)=2=2\cdot 1=2\cdot f(1)=\sqrt{4}\cdot f(1)=4^{\frac{1}{2}}\cdot f(1)$$ 

Für x=4 haben wir $$f(4) = 2 \ \text{ und } \ f(4\cdot 4)=4=2\cdot 2=2\cdot f(4)=\sqrt{4}\cdot f(4)=4^{\frac{1}{2}}\cdot f(4)$$ 

Für x=9 haben wir $$f(9) = 3 \ \text{ und } \ f(4\cdot 9)=6=2\cdot 3=2\cdot f(9)=\sqrt{4}\cdot f(9)=4^{\frac{1}{2}}\cdot f(9)$$

Wir sehen also dass $$f(4\cdot x)=4^{\frac{1}{2}}\cdot f(x)$$ und somit ist die Funktion homogen vom Grad 1/2.