Da diese Frage noch nicht zufriedenstellend beantwortet wurde, möchte ich
https://www.alpertron.com.ar/ECM.HTM
vorstellen.
Bis etwa 70 Stellen kann jede Zahl relativ schnell untersucht werden.
Oft wird jedoch einfach nur mit dem ECM-Algorithmus gesucht, wo es manchmal schnellere gibt.
Beispiel:
3761844347944019380812448477142805854310131054241322463562897739716154279181742220781
Faktorisierer | Berechnungszeit
---------------------+--------------------------
Pollard.., Williams, > 1 h (nicht abgewartet!)
Carmich..., > 1 h (nicht abgewartet!)
Mathematica > 1 h (nicht abgewartet!)
alpertron.com 18 min 48 s
yafu\siqs 8 Threads 55.7 s
Fermat GMP 1 Thread 1.01s
Noch was zur Stellenanzahl:
Wenn sich eine zu untersuchende Zahl für den Carmichael-Test eignet, sind 9000 Stellen kein Problem!
Wenn es jedoch eine echte RSA-Zahl ist, gibt es bereits 260stellige wie
https://en.wikipedia.org/wiki/RSA_numbers#RSA-260
die bis heute nicht gefunden wurden (also Jahre Suchzeit mit schnellen Computern)!!!
Grüße
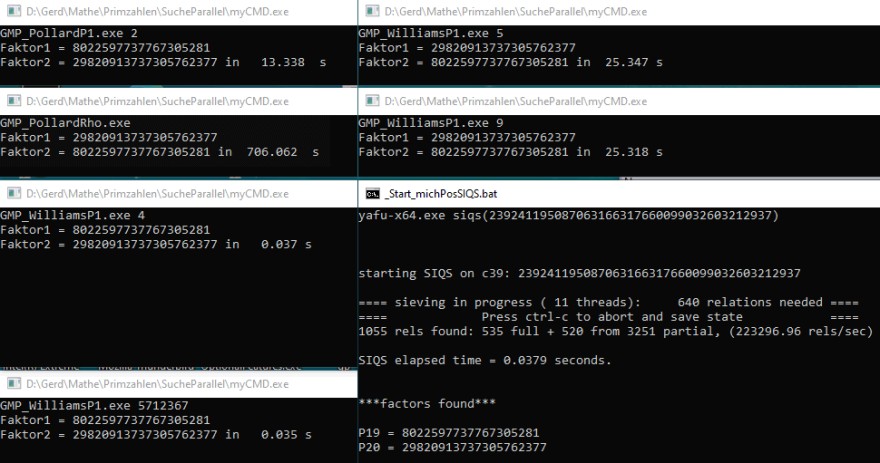
Mittlerweile habe ich noch etwa 10 weitere Algorithmen gefunden (oder bekannte programmiert), die alle meist zwischen
diesen beiden Extremen liegen. Ich starte einfach alle 16 parallel und beobachte, welcher am schnellsten antwortet
(aber lokal, also nicht online)